Moyenne arithmétique et moyenne géométrique
Test préliminaire
Pour profiter au maximum de cette page, essayez de répondre à la question suivante :
Sachant cela, auriez-vous mieux fait il y a cinq ans d'investir dans un produit indiciel indexé sur le CAC ou de garder vos sous bien à l'abri sous votre matelas ?
Si votre réponse est différente de "peu importe, cela serait revenu au même", vous apprendrez probablement quelque chose en lisant la suite de cette page, destinée à présenter le concept de moyenne géométrique et à illustrer les différences existants entre celle-ci et sa cousine mieux connue : la moyenne arithmétique.
Moyenne arithmétique
Tout le monde connaît la moyenne arithmétique, c'est elle qui permet de calculer sa moyenne à l'école par exemple. Elle consiste à diviser la somme des éléments par le nombre d'éléments.
La moyenne arithmétique d'une liste de n données se calcule de la manière suivante :
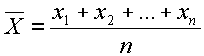
Tout le monde a tendance à l'appliquer partout où il est question de moyenne. Ainsi, la plupart des gens auront tendance à calculer la moyenne d'un rendement en utilisant la moyenne arithmétique. Ce qui nous donnerait pour l'exemple du CAC ci-dessus :
| Année | Valeur du CAC à la fin de l'année | Rendement | Rendement arrondi |
|---|---|---|---|
| 1997 | 2998.91 | ||
| 1998 | 3942.66 | +31.47% | +31% |
| 1999 | 5958.32 | +51.12% | +51% |
| 2000 | 5926.42 | -0.54% | -1% |
| 2001 | 4624.58 | -21.97% | -22% |
| 2002 | 3063.91 | -33.75% | -34% |
| Somme des rendements | 26.34% | 25% | |
| Moyenne arithmétique | 5.27% | 5% | |
Soit un rendement annuel de 5%. Si l'on avait perçu 5% de rendement par an, après cinq ans, en plaçant 10 000 euros, on aurait gagné 2 762,82 euros comme l'indique le tableau suivant :
| Année | Rendement | Capital |
|---|---|---|
| 1997 | 10 000,00 | |
| 1998 | +5% | 10 500,00 |
| 1999 | +5% | 11 025,00 |
| 2000 | +5% | 11 576,25 |
| 2001 | +5% | 12 155,06 |
| 2002 | +5% | 12 762,82 |
La dure réalité
Malheureusement, la réalité est toute autre. Si l'on avait placé 10 000 euros sur le CAC40 fin 1997, on disposerait aujourd'hui de 10 216,75 euros, comme le montre le tableau ci-dessous :
| Année | Valeur CAC | Rendement | Capital |
|---|---|---|---|
| 1997 | 2998,91 | 10 000,00 | |
| 1998 | 3942,66 | +31,47% | 13 146,98 |
| 1999 | 5958,32 | +51,12% | 19 868,29 |
| 2000 | 5926,42 | -0,54% | 19 761,91 |
| 2001 | 4624,58 | -21,97% | 15 420,87 |
| 2002 | 3063,91 | -33,75% | 10 216,75 |
On aurait donc gagné 216,75 euros en cinq ans. Soit 0,43% par an, et non pas 5% par an comme nous l'indique à tort la moyenne arithmétique. On peut d'ailleurs le voir sur le graphique ci-dessous. La ligne verte montre la progression du CAC40, la ligne bleue montre une progression constante de 0,43% et la ligne rouge une progression constante de 5%, le tout pour une base de départ identique égale à 2 998,91, c'est à dire à la valeur du CAC au 31/12/1997 :
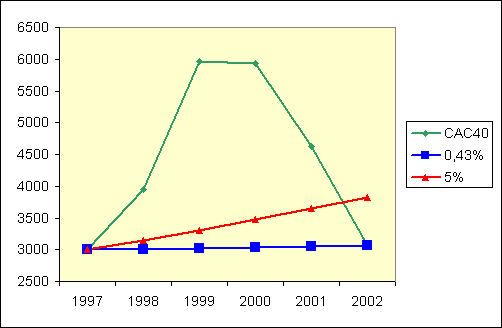
Pourquoi ? Pourquoi la moyenne arithmétique ne fonctionne pas ? Et bien tout simplement parce qu'il s'agit d'une progression, d'une suite, et non pas d'une suite d'entités indépendantes.
Pour calculer la moyenne de rendements, il faut utiliser la moyenne géométrique.
Moyenne géométrique
La moyenne géométrique d'une suite de données xn est calculée de la manière suivante :
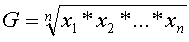
Dans notre exemple du CAC40 sur cinq ans, on obtient :
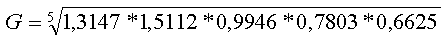
Soit :
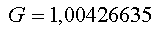
C'est à dire 0,43% en arrondissant.
Et avec Excel ?
Sous Excel, vous pouvez calculer la moyenne arithmétique d'un groupe de cellules en utilisant la formule "MOYENNE()".
Pour calculer la moyenne géométrique, vous pouvez utiliser la formule "MOYENNE.GEOMETRIQUE()". Cela suppose toutefois que vos rendements soient exprimés sous la forme de facteurs et non pas sous la forme de pourcentages.
Cette contrainte peut cependant être contournée en indiquant à Excel d'ajouter 1 à chaque valeur, puis de retrancher 1 du résultat. Ceci peut se faire de la manière suivante, par exemple pour calculer la moyenne géométrique des cellules A1 à A4 :
=MOYENNE.GEOMETRIQUE(1+A1:A4)-1
Il faut alors saisir la formule sous la forme matricielle en prenant soin de la valider en appuyant simultanément sur les touches SHIFT, CONTROL et ENTREE, plutôt qu'en appuyant uniquement sur ENTREE.
Autre possibilité, utiliser la fonction ci-dessous :
'**************************************************************************** '* Fonction CalculeMoyenneGeometrique * '**************************************************************************** '* * '* DESCRIPTION : calcule la moyenne géométrique d'une plage de valeurs * '* exprimées sous la forme de pourcentages, donc susceptibles * '* d'être négatives. * '* * '* ENTREE..... : r = plage de valeurs. * '* * '* SORTIE..... : Neant. * '* * '* RETOUR..... : Moyenne géometrique de la plage de valeurs. * '* * '**************************************************************************** Function CalculeMoyenneGeometrique(r As Range) As Double '----- On multiplie tous les facteurs entre eux ----- dblTotal = 1 For i = 1 To r.Count dblTotal = dblTotal * (r.Cells(i, 1) + 1) Next i '----- On prend ensuite la racine nième du produit calculé ----- dblTotal = dblTotal ^ (1 / r.Count) '----- On renvoie la valeur calculée ---- CalculeMoyenneGeometrique = dblTotal - 1 End Function
Attention, il s'agit d'une fonction et pas d'une macro. Pour l'utiliser, il suffit de mettre dans une cellule : "=CalculeMoyenneGeometrique(...)".
![]() Item suivant : l'ordre des rendements
Item suivant : l'ordre des rendements
![]() Retour au début de la page
Retour au début de la page
![]() Retour au sommaire des choses à savoir
Retour au sommaire des choses à savoir
![]() Retour au sommaire du site
Retour au sommaire du site
Rubriques
Meilleurs courtiers en Bourse
Meilleurs PEA
Toutes les données du CAC40
Livres finance et Bourse
Newsletter
Pour recevoir nos derniers articles, détachements de dividendes et offres de placements :
Nous contacter ou nous suivre sur les réseaux
Site hébergé par OVH - 2 rue Kellermann - 59100 Roubaix - France - Tel : 09 72 10 10 10