Le classeur 'Optimisation.xls'

Sommaire

Le classeur "Optimisation.xls"

Avertissement important

Les données de rendement et de variance des variations de rendement (ie risque) utilisées dans ce classeur sont des données passées. Elles sont utilisées ici dans un but pédagogique. Il faut garder à l'esprit qu'aussi bien les rendements des valeurs mobiliéres que les variances de leurs variations ne sont pas constants dans le temps. Leurs pouvoirs prédictifs sont donc pour le moins douteux.

Voici d'ailleurs ce qu'en disent deux auteurs.

Florin Aftalion dans La Nouvelle Finance et la Gestion des Portefeuilles (pages 68 à 70) :

[...] l'investisseur doit appliquer le modèle de Markowitz à l'aide d'estimations obtenues sur un échantillon de rentabilités passées, alors que c'est un autre échantillon qui déterminera la frontière représentant les portefeuilles efficients effectivement gérés. Le hic est qu'il est impossible de connaître à l'avance les paramètres (espérances de rentabilité, variances et covariances) de cette frontière efficiente là.

Le choix de portefeuilles efficients pose donc le problème du "risque d'estimation" lorsque le modèle de Markowitz est mis en oeuvre à l'aide de données historiques (mais peut-on faire autrement ?).

[...]

Jobson et Korkie concluent que l'application pratique du modèle de Markowitz au choix des portefeuilles ne donne pas de meilleurs résultats que ceux qui seraient obtenus par la sélection systématique de portefeuilles équipondérés.

[...]

Cependant, lorsque des contraintes de non-négativité sont imposées, les rentabilités des portefeuilles optimaux ne sont plus aussi sensibles aux variations des espérances des rentabilités des titres (contrairement à leur composition).

[...]

(toutes choses égales par ailleurs) les erreurs commises sur les rentabilités espérées des titres ont un impact sur la rentabilité des portefeuilles optimaux beaucoup plus important que les erreurs sur les variances et les covariances (10 à 20 fois plus fortes pour les mêmes variations en pourcentage des moyennes ou des variances-covariances).

Compte-tenu de ces constatations, le modèle de Markowitz (ou l'optimisation moyenne-variance) ne peut servir à la gestion de portefeuilles sans que son domaine d'application ne soit restreint ou que des correctifs ne lui soient apportés.

A propos de la première catégorie de mesures, il convient de noter que de tous les portefeuilles composant une frontière efficiente, celui correspondant à la variance minimum est le seul dont la composition ne dépend que des variances-covariances des titres qui le composent. Ce portefeuille, n'étant pas soumis aux effets des erreurs de mesure sur les moyennes, est beaucoup plus stable que ceux constituant le reste de la frontière efficiente (au cours des périodes de gestion, il reste proche du "vrai" portefeuille de variance minimum). Il peut donc paraître préférable de n'investir que dans des portefeuilles de variance minimum !

Notons également que l'ensemble de la frontière efficiente (surtout si des contraintes de non négativité sont imposées) gagne en stabilité si deux conditions sont remplies : les estimations sont effectuées sur de très longues périodes et les rentabilités comme les variances des actifs constitutifs sont plus dissemblables. Cette dernière condition est satisfaite pour les portefeuilles composés de classes d'actifs tels que bons du Trésor, obligations, actions et biens immobiliers. Comme les paramètres de ces classes d'actifs se prêtent à des estimations sur de très longues périodes, la frontière efficiente que décrivent les portefeuilles qui en sont composés sont relativement stables. Des institutions telles que les fonds de retraite qui mettent en oeuvre ces portefeuilles peuvent donc légitimement appliquer les résultats d'analyses espérance-variance (Boulier et Dupré, 2002).

Et Robert Haugen dans The New Finance (page 11) :

It is possible to build stock portfolios that have the lowest possible risk, given your objective for expected return. Call the technique to build these portfolios The Tool.

[...]

There is nothing wrong with The Tool--other than the fact that almost no one uses it1.

[...]

1 Except at asset allocation levels where institutions such as pension funds use it to determine how much of their funds should be invested in asset classes like bonds and stock. The Tool is also used by quantitative investment managers to manage the volatility of the differences between the returns on their long and short portfolios. Hedge funds actually build portfolios of stocks that they sell short. Long only managers are "short" their benchmark like the S&P500 stock index.

Voilà pour l'avertissement. Souvenez vous donc que l'optimisation de portefeuille est un moyen, un outil, applicable uniquement dans certains contextes (long terme et allocation d'actifs plutôt qu'allocation de titres dans un portefeuille d'actions). Ce n'est pas le Graal de l'investisseur !

Let's go on...

Rhaaaaaaaa, enfin, nous y sommes. Après cette petite douche écossaise, nécessaire car il s'agit de vos sous, vous pouvez télécharger le classeur Excel en Cliquant ici.

Certaines versions francisées du fichier SOLVER.XLA posent des problèmes à l'exécution des macros faisant appel au solveur.Si lors de l'exécution des macros d'optimisation sous Office XP vous obtenez un message d'erreur du style "Erreur de compilation: Sub ou Fonction non définie", utilisez cette autre version du classeur ou suivez les procédures de contrôles de bonne configuration du solver dans la partie En cas de problème

.

Pour pouvoir optimiser un portefeuille, il nous faudra :

  • un portefeuille, c'est à dire la liste des valeurs que nous acceptons d'acquérir. Je vous propose de restreindre notre univers à celui des sociétés du CAC40 et de quelques grands indices. Vous pourrez ensuite adapter l'exemple à vos propres besoins.
  • les rendements et les variances des rendements espérés pour chacune de ces valeurs. On peut ici utiliser soit des rendements espérés, soit ceux historiquement constatés.
  • la matrice de variance/covariance des rendements des différentes valeurs. On peut ici aussi soit la calculer en fonction des données passées, soit la fabriquer en fonction d'autres éléments comme par exemple les variances et covariances des secteurs auxquels les valeurs appartiennent.

Pour faire simple, vous permettre d'adapter le classeur à vos besoins et ne pas vous torturer les méninges à estimer des rendements futurs, j'ai décidé de permettre de travailler sur des données passées. Attention toutefois : ceci ne permet probablement pas l'obtention des meilleurs résultats.

Le classeur se compose donc de quatre feuilles et de plusieurs macros :

  • une feuille rappelant le mode d'emploi du classeur.
  • une feuille de données permettant de calculer, depuis les cours de cloture mensuels, le rendement moyen, ainsi que la variance des rendements de chaque valeur.
  • une feuille destinée à contenir la matrice de variance/covariance des rendements mensuels des différentes valeurs.
  • une feuille contenant le portefeuille à optimiser et permettant de tracer la frontière efficiente de l'univers de valeurs susceptible de le composer.
  • une macro permettant de calculer la matrice de variance/covariance à partir des données passées.
  • un ensemble de macros permettant d'automatiser l'utilisation du solveur pour optimiser un portefeuille et pour tracer la frontière efficiente d'un univers de valeurs.

Feuille "Données"

Paires de colonnes Cette feuille est composée de paires de colonnes, une par valeur de notre univers. La première colonne de chaque paire contient le cours de cloture de la valeur à la date indiquée dans la colonne de gauche de la feuille, et la seconde colonne de chaque paire donne le rendement obtenu par la valeur en question sur la dernière période.
Dans notre exemple, les périodes sont mensuelles.
Les rendements sont indiqués sous la forme de facteurs et non pas de pourcentages de manière à pouvoir utiliser la fonction MOYENNE.GEOMETRIQUE() d'Excel pour calculer le rendement moyen.
La dernière ligne de chaque paire de colonnes indique le rendement moyen (moyenne géométrique des rendements des différentes périodes).

Feuille "VarCovar"

Cette feuille contient la matrice de variance/covariance des rendements des valeurs listées dans la feuille "Données".
La matrice de variance/covariance est générée automatiquement à la demande par la macro "CreeMatriceVarCovar". Pour l'exécuter, il suffit de cliquer sur le bouton correspondant dans la feuille "Mode d'emploi", ou de la sélectionner dans la liste des macros en cliquant sur 'Outils/Macro/Macros", puis en sélectionnant "CreeMatriceVarCovar" et en cliquant sur le bouton "Exécuter".

Feuille "Portefeuille"

Un dessin valant mieux que de grands discours, voici la feuille principale du classeur :

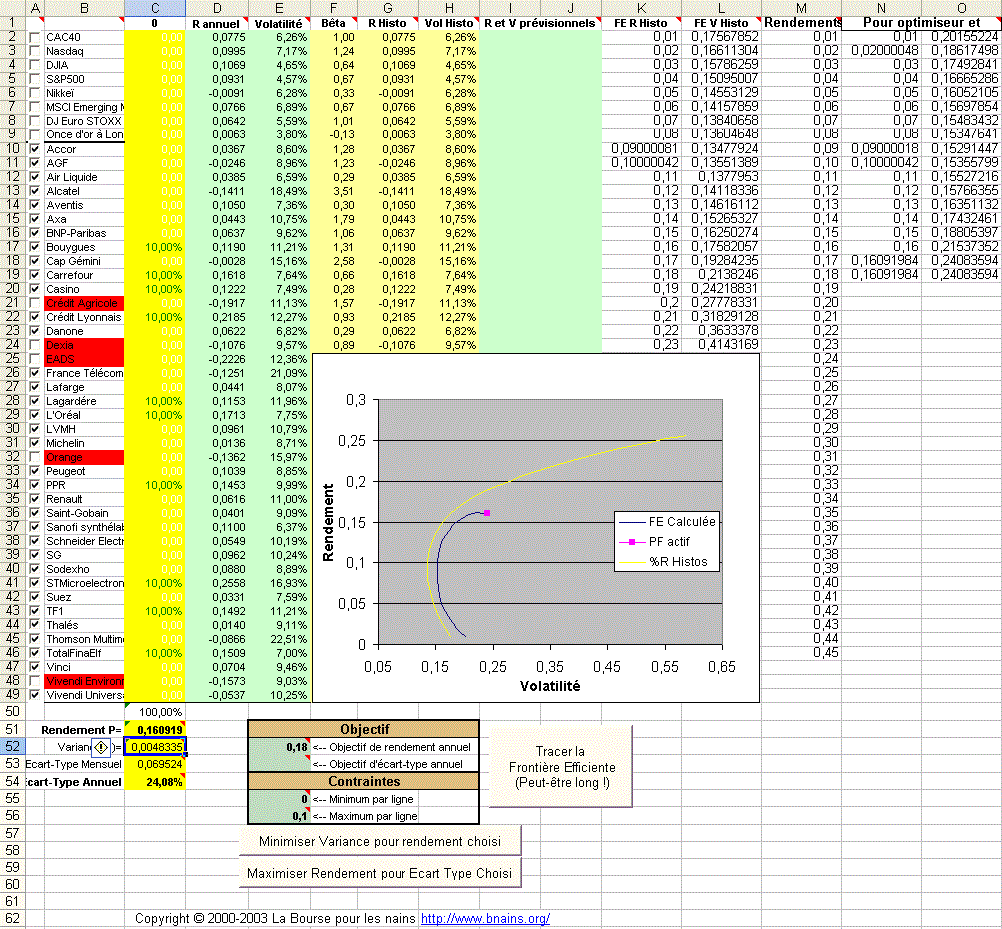
Photo d'écran de la feuille Excel d'optimisation

Et son mode d'emploi :

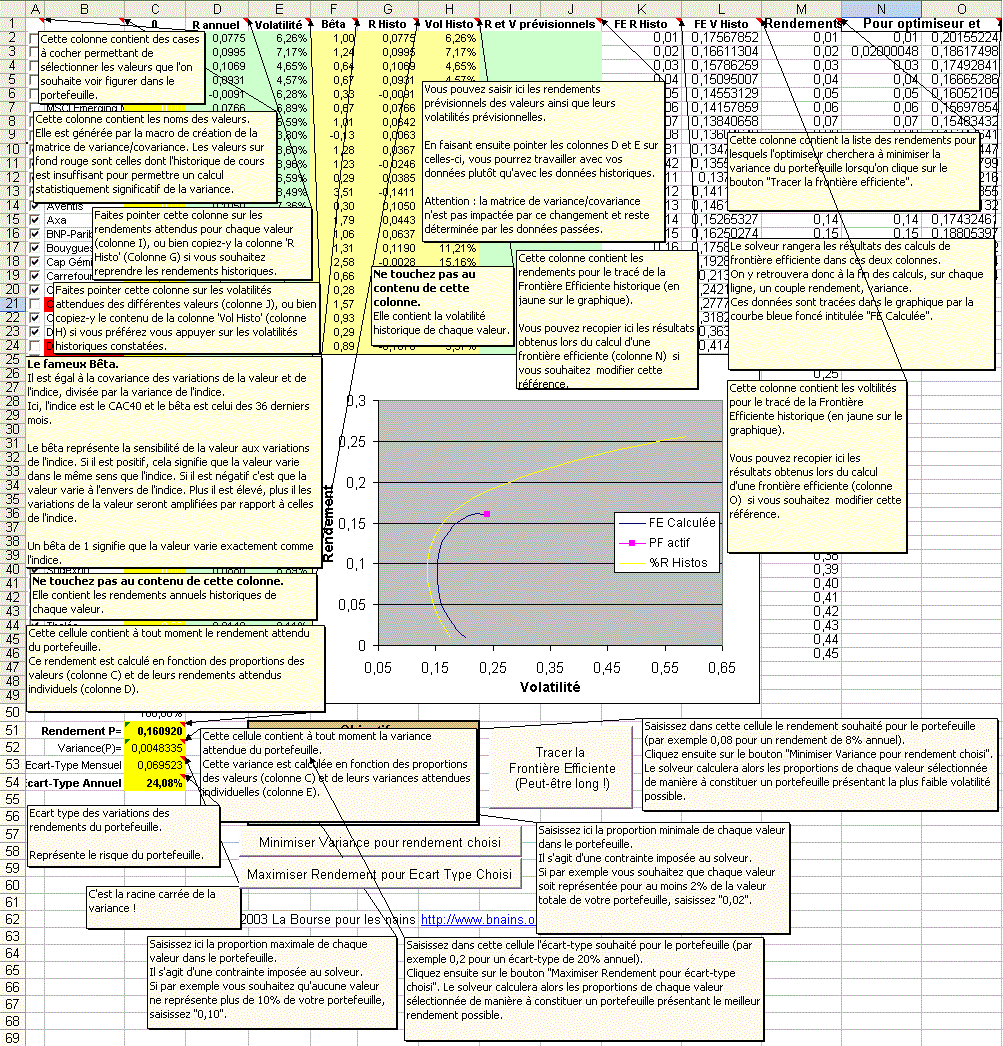
Photo d'écran de la même feuille Excel avec de nombreux commentairex explicitant les cellules

Partie haut-gauche

Colonne A :
La première colonne de cette feuille contient des cases à cocher, permettant de sélectionner les valeurs que l'on souhaite voir figurer dans le portefeuille. Les valeurs situées sur des lignes dont la case n'est pas cochée seront systématiquement exclues des portefeuilles constitués.

Colonne B :
La deuxième colonne contient les noms des valeurs.

Colonne C : "Proportion"
La troisième colonne est destinée à contenir les proportions de chaque valeur dans le portefeuille. Lorsqu'on optimise un portefeuille en cliquant sur le bouton "Optimiser PF", on retrouve dans ces colonnes les proportions calculées par l'optimiseur.
On peut aussi utiliser ces colonnes à l'envers. Si l'on saisit des proportions, par exemple correspondant à un portefeuille existant, on obtient le calcul du rendement et de la variance attendues de ce portefeuille et l'on peut voir sur le graphique où il se situe par rapport à la frontière efficiente.

Colonne D : "R annuel"
Cette colonne contient les rendements annuels espérés pour chaque valeur. Elle est utilisée comme entrée par l'optimiseur. Vous pouvez soit la remplir manuellement en indiquant pour chaque valeur le rendement annuel attendu (1 = 100%), soit la faire pointer sur la colonne "R Histo" qui contient le rendement annuel constaté pour chaque valeur.

Colonne E : "Volatilité"
Cette colonne contient les volatilités annuelles espérées pour chaque valeur. Elle est utilisée comme entrée par l'optimiseur. Vous pouvez soit la remplir manuellement en indiquant pour chaque valeur la volatilité annuelle attendue (1=100%), soit la faire pointer sur la colonne "Vol Histo" qui contient la volatilité mensuelle constatée pour chaque valeur.

Colonne F : "Bêta"
Cette colonne n'est pas utilisée pour les calculs. Elle indique, pour information, le bêta de chaque valeur par rapport au CAC40.

Colonne G : "R Histo"
Cette colonne contient les rendements historiques constatés des différentes valeurs. Ils sont calculés sur la feuille "Données" et repris ici. Cette colonne ne doit pas être modifiée (cela ne servirait à rien puisqu'on peut modifier la colonne D à la place, ou faire pointer la colonne D sur la colonne I, ce qui évite de perdre les saisies lorsque l'on souhaite revenir aux rendements historiques).

Colonne H : "Vol Histo"
Cette colonne contient les volatilités historiques constatées des différentes valeurs. Elles sont calculées sur la feuille "Données" et reprises ici. Cette colonne ne doit pas être modifiée (cela ne servirait à rien puisqu'on peut modifier la colonne E à la place ou faire pointer la colonne E sur la colonne J, ce qui évite de perdre les saisies lorsque l'on souhaite revenir aux volatilités historiques).

Colonne I :
Cette colonne est destinée à contenir les rendements de chaque valeur dans le cas où l'on ne souhaite pas utiliser les rendements historiques. Vous pouvez donc saisir ici les rendements espérés de chaque valeur puis faire pointer la colonne D sur cette colonne.

Colonne J :
Cette colonne est destinée à contenir les volatilités de chaque valeur dans le cas où l'on ne souhaite pas utiliser les volatilités historiques. Vous pouvez donc saisir ici les volatilités attendues de chaque valeur puis faire pointer la colonne E sur cette colonne.
ATTENTION : la matrice de variance/covariance n'est pas modifiée pour autant et reste basée sur les données historiques.

Colonne K : "FE R Histo"
Cette colonne contient les rendements historiques pour le tracé de la frontière efficiente historique. Elle correspond à un portefeuille constitué des valeurs du CAC40 sans celles disposant d'un historique de cours insuffisant (valeurs sur fond rouge).
Si vous souhaitez disposer d'une autre référence, vous pouvez modifier ces données, en y recopiant par exemple le contenu de la colonne 'M', après avoir effectué un calcul de frontière efficiente sur un ensemble de titres.

Colonne L : "FE V Histo"
Cette colonne contient les volatilités historiques pour le tracé de la frontière efficiente historique. Elle correspond à un portefeuille constitué des valeurs du CAC40 sans celles disposant d'un historique de cours insuffisant (valeurs sur fond rouge).
Si vous souhaitez disposer d'une autre référence, vous pouvez modifier ces données, en y recopiant par exemple le contenu de la colonne 'N', après avoir effectué un calcul de frontière efficiente sur un ensemble de titres.

Colonne M : "Rendements"
Cette colonne contient la liste des rendements pour lesquels un portefeuille optimisé sera calculé, lorsque vous cliquerez sur le bouton "Tracer la frontière efficiente". Si vous souhaitez raccourcir les temps de calcul, vous pouvez changer le nombre de rendements, augmenter l'écart entre ceux-ci ou vous arrêter avant les 45% actuels (bien trop optimistes !).
Note : il serait possible simplement d'indiquer uniquement la valeur de début, celle de fin et celle de l'incrément et de modifier la macro TracerFrontiereEfficiente() en conséquence, mais le résultat serait le même. D'autant que la macro s'arrête lorsqu'elle trouve deux rendements successifs identiques. Si cela se produit, cela veut dire qu'il est impossible d'obtenir le rendement souhaité avec les titres sélectionnés et les contraintes exprimées.

Colonnes N et O :"Pour optimiseur et calcul frontière efficiente"
Ces colonnes sont remplies par la macro de calcul de la frontiére efficiente. Pour chaque rendement de la colonne L, l'optimiseur essaiera de composer un portefeuille constitué des valeurs sélectionnées (colonne A) en minimisant sa variance (volatilité). Le rendement et la variance du portefeuille calculé sont recopiées par la macro respectivement dans les colonnes M et N.
Le contenu des colonnes M et N est utilisé dans le graphique, c'est la courbe bleue foncé intitulée "FE calculée".

Utilisation du classeur

Optimisation d'un portefeuille

Vous pouvez calculer le portefeuille optimal, soit en cherchant le portefeuille présentant le risque attendu le plus faible pour un rendement donné, soit en cherchant le portefeuille présentant le rendement espéré le plus élevé pour un risque donné.

Pour ce faire, vous devez :

  • cocher les valeurs dont vous acceptez qu'elles figurent dans votre portefeuille.
  • indiquer le rendement ou l'écart-type souhaité dans la cellule E52 ou E53 (en bas au milieu).
  • cliquer sur le bouton 'Minimiser variance pour rendement choisi' ou 'Maximiser rendement pour Ecart Type choisi' selon le cas.

Le solveur sera alors programmé et lancé. Après une période de calculs vous pourrez consulter les proportions de valeurs qu'il aura sélectionnées (colonne C), ainsi que le rendement et l'écart-type annuel espérés pour le portefeuille.

Vous pouvez exprimer des contraintes sur la composition du portefeuille en les indiquant dans les cellules E55 et E56. Elles permettent de forcer la proportion de chaque valeur à respecter un minimum et un maximum fixés. Pour forcer par exemple l'optimiseur à retenir entre 2% et 15% de chaque valeur dans les portefeuilles évalués, saisissez 0,02 comme minimum et 0,15 comme maximum.

Calcul et affichage de la frontière efficiente

Les différentes combinaisons de valeurs composant un portefeuilles sont en nombre fini, chaque combinaison permettant d'obtenir un couple (rendement,risque) particulier. Si l'on pointe sur un graphique tous les couples (rendement,risque) obtenus avec un univers de titres donnés, on s'aperçoit qu'ils ne sont pas répartis dans l'espace de manière aléatoire. Les portefeuilles optimisés se trouvent sur la frontière efficiente.

Vous pouvez tracer la frontiére efficiente d'un univers de portefeuilles composés des valeurs que vous avez choisi et respectants les contraintes que vous avez exprimé en cliquant sur le bouton "Tracer la frontière efficiente". Attention, le calcul peut être assez long.

Pour ceux qui souhaitent voir les macros sans télécharger la feuille Excel, ou qui ne disposent pas d'Excel pour les lire, la page suivante propose les les sources des macros.

En cas de problème

RAPPEL suite aux multiples mails reçus: le solveur bien que fourni systématiquement avec Excel est désactivé par défaut. Pour faire fonctionner l'optimisation, VOUS DEVEZ ACTIVER LE SOLVEUR !

Si l'optimisation ne fonctionne pas et que vous obtenez des messages d'erreur du type "Erreur de compilation ou bibliothèque introuvable", vérifiez que le solveur est bien installé et fonctionne correctement à l'aide de la procédure décrite dans les parties "Activation du solveur" et "Utilisation du solveur" de la page Optimisation, principes et pratique.

Et si vous obtenez toujours un message d'erreur lors du lancement des macros bien que le solveur fonctionne en mode interactif, contrôlez le fait que les références au solver pour VBA soient correctes en suivant les étapes décrites ci-dessous car il arrive qu'après des mises à jour d'Excel, les références pointent vers une version de fichier solver supprimée.

Vous avez ce message d'erreur ou un équivalent lors de l'exécution d'une macro du classeur Optimisation, par exemple lorsque vous essayez de générer la matrice de variances/covariances :

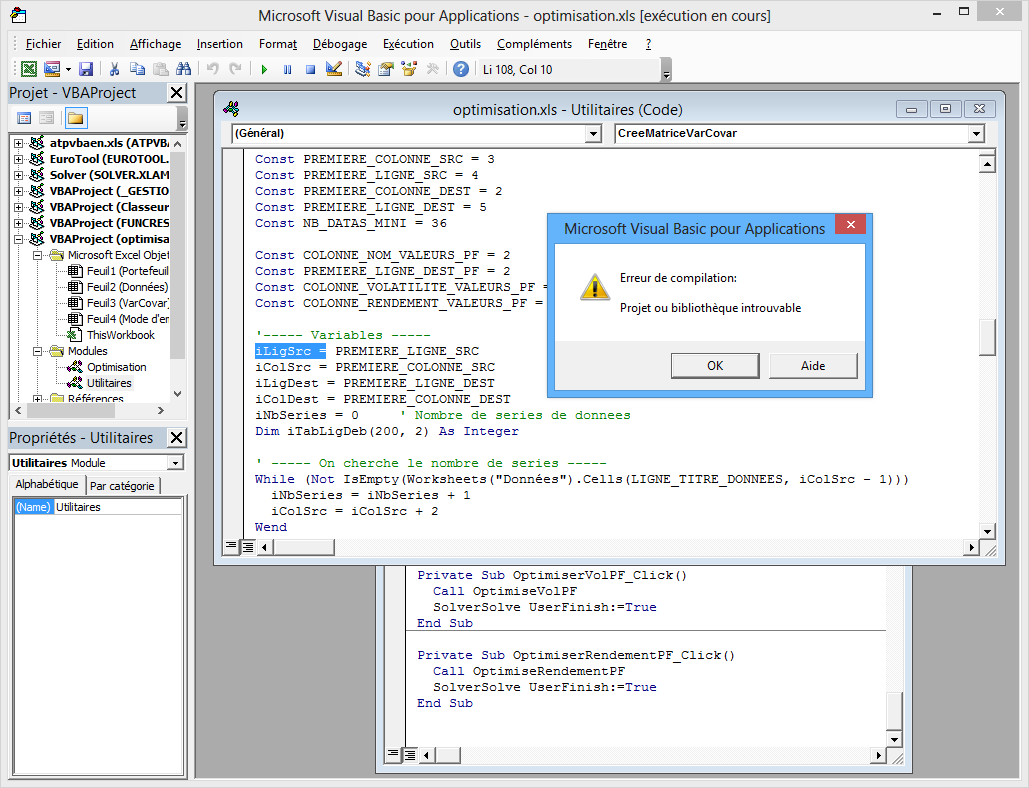
Boite de dialogue 'Erreur de compilation - Projet ou bibliotheque introuvable'.

Cliquez sur le bouton "OK", puis arrêtez l'exécution de la macro en cliquant sur le bouton d'arrêt de l'éditeur de macros (bouton bleu carré intitulé "Réinitialiser" :

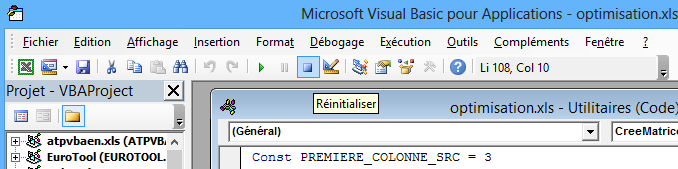
Bouton 'Réinitialiser' dans la barre d'outils de l'éditeur de macros.

Ensuite choisissez l'entrée "Références" du menu "Outils" :

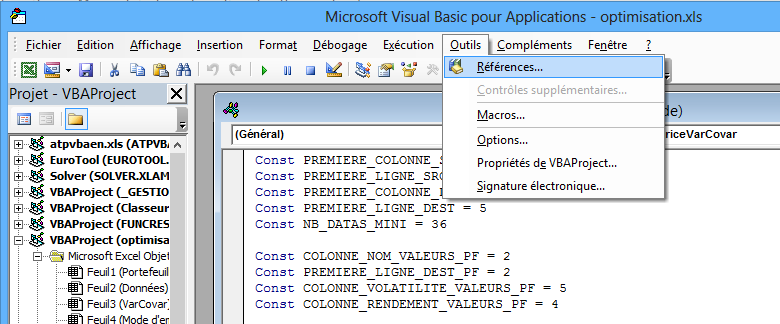
Entrée 'Références...' du menu 'Outils' de l'étditeur de macros.

Et vérifiez que vous avez bien une ligne cochée "MANQUANT : SOLVER.XLA" :

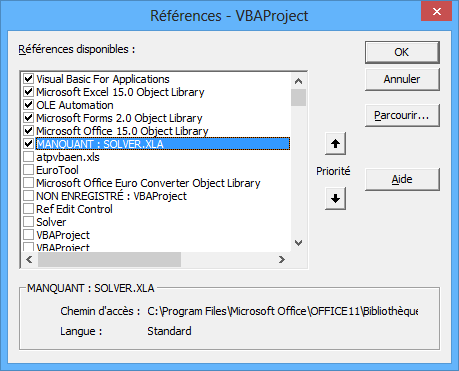
Boite de dialogue 'Références - VBAProject' contenant une ligne 'MANQUANT : SOLVER.XLA' cochée.

Décochez cette ligne, puis cochez la ligne "Solver" qui doit se trouver un peu plus bas :

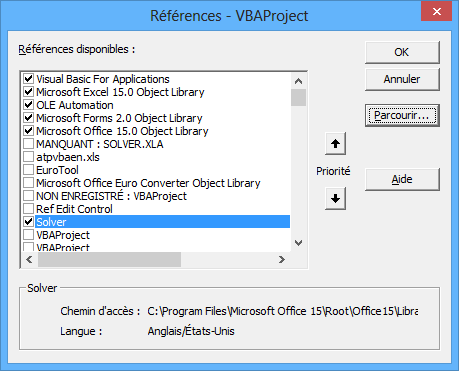
Boite de dialogue 'Références - VBAProject' avec la ligne 'MANQUANT : SOLVER.XLA' décochée et la ligne 'Solver' cochée.

Cliquez sur le bouton "OK", puis relancez la macro, tout devrait fonctionner correctement !

Et après ?

Après, après ? He bien, il faudrait s'attaquer au problème de l'instabilité des variances/covariances et à l'amélioration des prévisions de rendement. Mais ce n'est pas une mince affaire !
Concernant les variances/covariances, il existe des pistes, concernant les rendements, c'est beaucoup plus délicat.

Au préalable, il peut être intéressant de poursuivre un peu sur le chemin de la théorie en voyant comment il est possible d'obtenir un portefeuille situé dans le coin supérieur gauche ou supérieur droit du graphique, c'est à dire au-delà de la frontiere efficiente. Si, si, c'est possible ! Il sera toujours temps ensuite de revenir sur les problèmes plus ardus nécessitant une boule de cristal.

Vous pouvez donc poursuivre via la page le levier et l'optimisation de portefeuille.

Puce rouge Retour au début de la page   Puce rouge Retour au sommaire de l'optimisation   Puce rouge Retour au sommaire du site

Rubriques

Meilleurs courtiers en Bourse
Meilleurs PEA
Toutes les données du CAC40
Livres finance et Bourse

  Newsletter

Pour recevoir nos derniers articles, détachements de dividendes et offres de placements :

S'abonner à la newsletter

Nous contacter ou nous suivre sur les réseaux

Site hébergé par OVH - 2 rue Kellermann - 59100 Roubaix - France - Tel : 09 72 10 10 10