Optimisation de portefeuille financier : le levier
Sommaire
- La frontière efficiente
- Optimisation
- Le principe
- Optimisation : la pratique
- Activation du solveur
- Utilisation du solveur
- Le classeur "Optimisation.xls"
-
- Avertissement important
- Let's go on...
- Feuille "Données"
- Feuille "VarCovar"
- Feuille "Portefeuille"
- Utilisation du classeur
- Optimisation d'un portefeuille
- Calcul et affichage de la frontiere efficiente
- Annexe : les macros
- Création de la matrice de variances/covariances
- Optimisation d'un portefeuille
- Et après ?
-
- Le levier Vous êtes ici !
- Cas d'un portefeuille mono-valeur
- Portefeuilles situés au-delà de la frontière efficiente
- Levier et Optimisation de portefeuille
- Retour sur le risque
- Le levier : une arme à double tranchant
- Dissymétrie des gains et des pertes
- Morale de l'histoire
- Cas d'un portefeuille mono-valeur
Le levier
Après avoir vu la frontière efficiente et l'optimisation de portefeuille, on peut s'intéresser au levier, lequel permettra de constituer des portefeuilles situés au-delà de la frontière efficiente.
Cas d'un portefeuille mono-valeur
Un portefeuille constitué uniquement de liquidité serait représenté sur notre graphe (rendement,risque) par un point situé aux coordonnées (0,0). En effet ce portefeuille présenterait bien un risque nul pour un rendement égal lui-aussi à zéro.
Un portefeuille constitué uniquement d'une valeur, par exemple Carrefour serait représenté sur notre graphe par le point représentant la valeur Carrefour. En effet ce portefeuille présenterait bien le même risque que la valeur Carrefour pour le même rendement qu'elle.
En traçant un segment de droite entre ces deux points, on obtient l'univers de portefeuilles constitués d'une partie investie dans la valeur Carrefour et du reste conservé en liquidité :
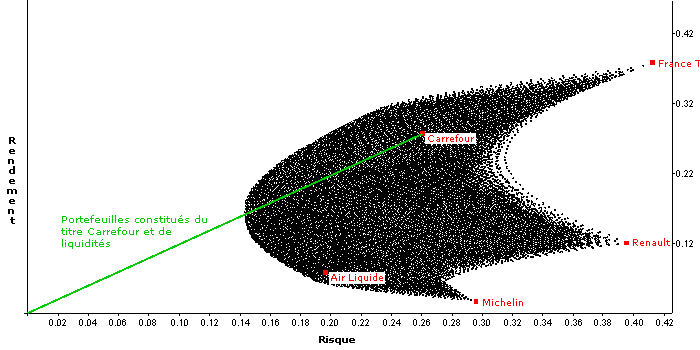
Pour améliorer le rendement des portefeuilles contenant une part de liquidité, il est possible d'investir cette part dans un placement monétaire sans risque (qu'on appelle généralement "avoir sans risque"). En imaginant que l'avoir sans risque présente un rendement de 3%, l'univers des portefeuilles constitués d'une partie investie dans la valeur Carrefour et du reste dans l'avoir sans risque devient :
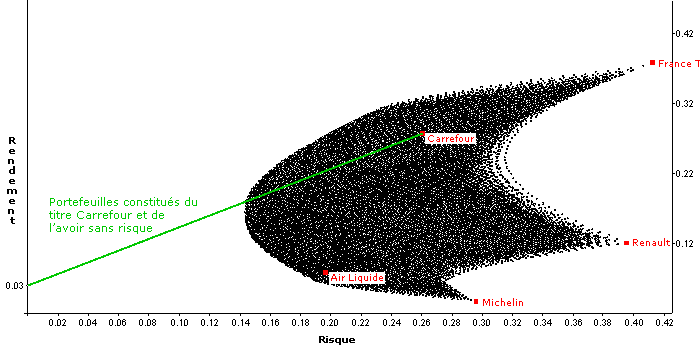
Le portefeuille constitué en totalité de l'action Carrefour présente un levier de 1. C'est à dire qu'on a une exposition au risque égale à 1 fois le risque des titres détenus. Tous les portefeuilles composés d'une part non nulle d'avoir sans risque ou de liquidités présentent un levier inférieur à 1.
En empruntant de l'argent, il est possible d'acheter des actions Carrefour pour davantage de capital que celui détenu. On peut donc constituer un portefeuille dont le levier sera supérieur à 1 et prolonger le segment représentant l'univers de portefeuilles Carrefour pour le transformer en demi-droite :
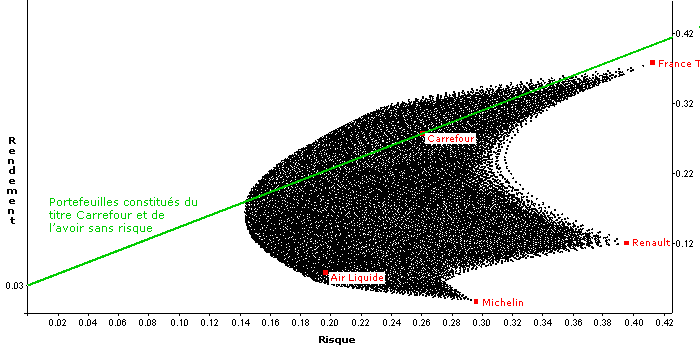
En fait la demi-droite représentant les portefeuilles constitués de titres Carrefour avec des leviers supérieurs à 1 devrait présenter une pente plus abrupte que celle affichée. Elle devrait prolonger la demi-droite passant par le portefeuille sans risque et le point 0,0. Toutefois si l'on considère que l'emprunt a un coût dont le taux est égal à l'avoir sans risque, alors la représentation est correcte.
Portefeuilles situés au-delà de la frontière efficiente
Avec un levier suffisamment important il est possible de constituer un portefeuille Carrefour situé au-delà de la frontière efficiente. Par exemple un portefeuille composé exclusivement de titres Carrefour pour un montant égal à 1,5 fois notre capital présenterait un rendement de 40,17% pour un risque de 38,72% :
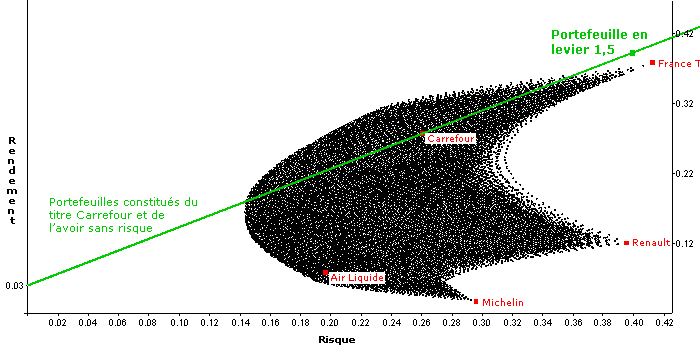
Sans recours au levier il est impossible de créer un portefeuille présentant ce rapport rendement/risque puisque l'univers de portefeuilles constitué avec nos cinq valeurs ne couvre pas cette zone. Le levier peut donc nous aider à dépasser la frontière efficiente. Et cela fonctionne bien évidemment dans les deux sens : en levier supérieur à 1 pour obtenir des rendements qu'aucun portefeuille de notre univers ne pourrait nous donner ou en levier inférieur à 1 pour obtenir des risques inférieurs.
Evidemment on peut emprunter de l'argent et adopter un levier supérieur à 1 avec n'importe quel portefeuille de notre univers de départ (constitué uniquement des 5 valeurs Air Liquide, Carrefour, France Télécom, Renault et Michelin), ce qui augmenterait à la fois le rendement et le risque du portefeuille en question. Mais cette situation ne serait pas optimale, ce que le chapitre suivant devrait démontrer.
Levier et optimisation de portefeuille
Maintenant que l'on a vu comment constituer un portefeuille situé au-delà de la frontière efficiente, il serait bon de combiner cela avec l'optimisation de portefeuille. Si l'on trace une demi-droite tangente à la frontière efficiente et passant par le portefeuille constitué exclusivement de l'avoir sans risque, on obtient l'univers des portefeuilles constitués d'une combinaison du portefeuille le plus efficient et de l'avoir sans risque. Ces portefeuilles sont représentés sur le segment de droite vert du graphique ci-dessous. On peut aussi constituer des portefeuilles constitués exclusivement du portefeuille efficient, mais en levier supérieur à 1, c'est à dire avec un investissement supérieur à son capital (en empruntant de l'argent donc, ou en utilisant des options). Ces portefeuilles sont représentés sur le segment de droite orange du graphique ci-dessous. Les portefeuilles situés sur cette droite présentent les meilleurs couples (rendement,risque) que l'on puisse obtenir. Il n'est pas possible de créer un portefeuille situé au-dessus et à gauche de la droite verte et orange.
En jouant sur le levier (et la constitution du portefeuille pour un levier inférieur à 1), il est dès lors possible de choisir son rendement souhaité ou son risque souhaité et d'en dériver le portefeuille idéal, qui présentera selon le cas un levier inférieur ou supérieur à 1 :
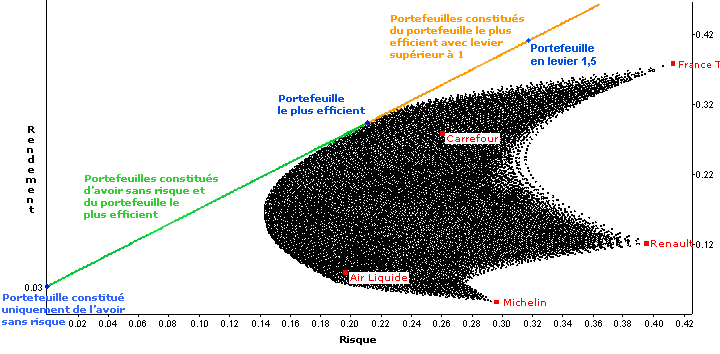
A titre d'exemple, sur le schéma ci-dessus on voit bien qu'un levier 1,5 appliqué sur le portefeuille situé à la tangente entre la frontière efficiente et l'avoir sans risque permet d'obtenir un rendement presque identique avec un risque largement inférieur à notre portefeuille Carrefour en levier 1,5 de l'exemple précédent. En effet, un levier 1,5 appliqué sur le portefeuille "efficient" donne un rendement de 41,25% pour un risque de 31,5% (à comparer au rendement de 41,7% pour un risque de 38,72% présentés par le portefeuille Carrefour en levier 1,5). Pour le même risque de 38,7%, on pourrait obtenir un rendement de 50,02%, soit 8,32% de plus avec le portefeuille efficient et le même levier. Pour le même rendement de 41,7% on pourrait obtenir un risque de 31,87%, soit 6,83% de moins avec le portefeuille efficient et le même levier.
Pour bien enfoncer le clou, on peut encore observer les deux illustrations suivantes :
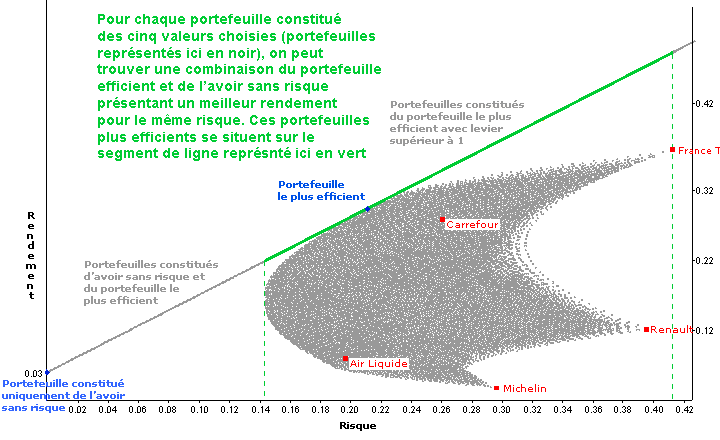
Pour tout portefeuille constitué de notre univers de 5 valeurs, on peut trouver un portefeuille au-delà de la frontière efficiente qui présentera un risque identique mais avec un rendement supérieur. Il suffit de se projeter verticalement sur le segment de droite rouge représentant les portefeuilles les plus efficients que l'on puisse construire, soit en combinant le portefeuille le plus efficient et l'avoir sans risque, soit en investissant dans le portefeuille le plus efficient avec un levier supérieur à 1.
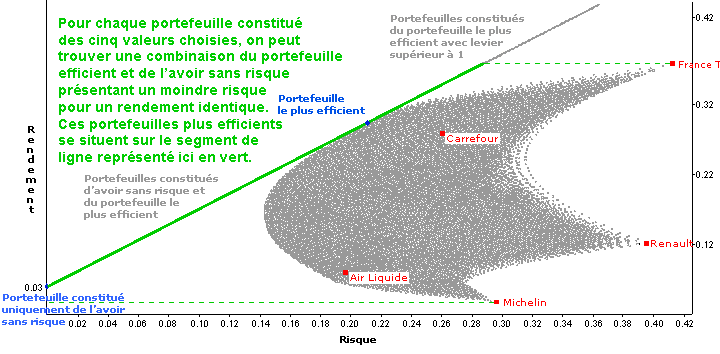
Pour tout portefeuille constitué de notre univers de 5 valeurs, on peut trouver un portefeuille au-delà de la frontière efficiente qui présentera un rendement identique mais avec un risque inférieur. Il suffit de se projeter horizontalement sur le segment de droite rouge représentant les portefeuilles les plus efficients que l'on puisse construire, soit en combinant le portefeuille le plus efficient et l'avoir sans risque, soit en investissant dans le portefeuille le plus efficient avec un levier supérieur à 1.
La constitution de portefeuilles composés de combinaisons d'avoir sans risque et du portefeuille le plus efficient de l'univers de valeurs considérées au départ permet de dépasser la frontière efficiente représentée en orange dans le graphique ci-dessous, qui devient ainsi une droite représentée en vert :
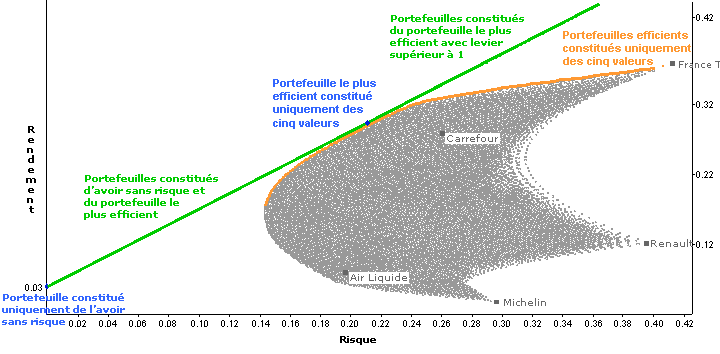
Finalement, on peut tirer de ces observations un mode opératoire de constitution de portefeuille consistant à suivre les étapes suivantes :
- Déterminer la composition idéale de votre portefeuille pour obtenir le meilleur rapport rendement/risque, ce qui revient à sélectionner le portefeuille situé au point de tangente entre la frontière efficiente et l'avoir sans risque ;
- Régler le levier pour ajuster le risque pris ou s'aligner sur le rendement souhaité. Le levier peut bien entendu être inférieur à 1.
Note : nous amenderons ces règles un peu plus loin. Continuez donc votre lecture ;-).
Retour sur le risque
A ce stade, il est nécessaire de revenir sur la notion de risque car il est très tentant d'utiliser des leviers supérieurs à 1, mais il impératif de bien saisir les risques associés.
Le levier : une arme à double tranchant
Le levier est une arme à double tranchant dans la mesure où s'il amplifie bien les mouvements de marché qui vont dans le sens espéré, il amplifie de la même manière les mouvements inverses. Ainsi en levier 3, une baisse de plus de 33% des actifs représentés par le portefeuille se soldera par la ruine !
Et ce n'est pas tout, car une baisse supérieure peut même se solder par des dettes selon le véhicule d'investissement employé !!!
Dissymétrie des gains et des pertes
Pour bien comprendre les risques associés au levier, il est intéressant de prendre conscience de la dissymétrie existant entre les gains et les pertes et du facteur d'accélération que constitue le levier vis à vis de cette dissymétrie.
Ainsi, en levier 1, lorsque vous perdez 50% de votre capital, vous devez réaliser une progression de 100% ensuite pour revenir à votre point de départ. En levier 2 une baisse de 50% vous ruine.
Exemple encore plus parlant : une baisse de 40% en levier 1 sera effacée par une hausse ultérieure de 66,66%. En levier 2 il faudra une hausse de 500% pour effacer une baisse de 40%.
Poussons un peu plus loin : en levier 1 une baisse de 30% sera effacée par une hausse de 42,86%. En levier 3 il faudra une hausse de 1000% pour effacer une baisse de 30%.
Toujours plus loin : en levier 1 une baisse de 19% sera effacée par une hausse de 23,46%. En levier 5 il faudra une hausse de 2000% pour effacer une baisse de 19% !!!
Le tableau ci-dessous indique les hausses nécessaires pour revenir à l'équilibre après une baisse donnée selon le levier employé :
| Gain nécessaire pour revenir à zéro selon levier | ||||||
|---|---|---|---|---|---|---|
| Perte | Levier 1 | Levier 2 | Levier 3 | Levier 4 | Levier 5 | Levier 10 |
| 10% | 11,11% | 25,00% | 42,86% | 66,67% | 125,00% | Ruiné ! |
| 20% | 25,00% | 66,67% | 150,00% | 400,00% | Ruiné ! | Ruiné ! |
| 30% | 42,86% | 150,00% | 900,00% | Ruiné ! | Ruiné ! | Ruiné ! |
| 40% | 66,67% | 400,00% | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! |
| 50% | 100,00% | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! |
| 60% | 150,00% | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! |
| 70% | 233,33% | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! |
| 80% | 400,00% | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! |
| 90% | 900,00% | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! |
| 100% | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! | Ruiné ! |
Le graphique ci-dessous illustre pour certains leviers les gains nécessaires pour revenir à zéro en fonction des pertes subies :
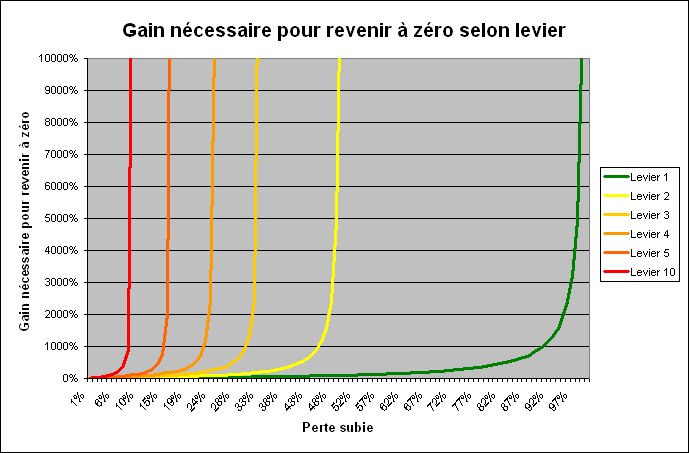
Un zoom sur le coin bas droit du graphique permet de bien apprécier la vitesse avec laquelle le levier accentue la dissymétrie des pertes et des gains :
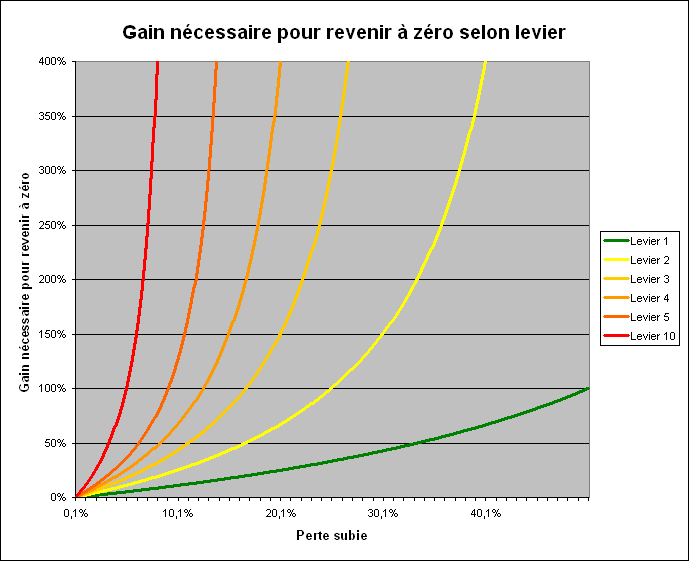
Morale de l'histoire
Si vous avez lu les pages consacrées au risque, vous devez avoir compris qu'il est impossible d'espérer obtenir un rendement important sans prendre de risques. Mais quel que soit votre objectif en terme de rendement, vous devez garder en tête le fait qu'il sera impossible de l'atteindre sans capital. Le scénario à éviter absolument est donc celui qui vous mène à la ruine.
Au-delà de la ruine, vous devez aussi éviter deux autres écueils : vous trouver dans une situation où un temps infini est nécessaire pour revenir à l'équilibre et vous trouver dans une situation où vous ne dormez plus tellement le sort de votre portefeuille vous préoccupe.
Eviter ces deux situations suppose d'une part d'avoir correctement anticipé les risques associés à un portefeuille et au levier employé et d'autre part d'avoir mené un travail d'introspection pour connaître votre limite de tolérance au risque. Cela suppose aussi et surtout d'utiliser le levier comme un potentiomètre de risque et non pas comme un potentiomètre de rendement. Pour éviter les deux écueils ci-dessus, le levier doit être envisagé comme un curseur permettant de régler le niveau de risque de votre portefeuille. L'utiliser comme un curseur permettant de régler le rendement attendu du portefeuille est le meilleur moyen pour vous conduire à la ruine ou à une longue succession de nuits blanches.
A la lumière de ces constats, nos règles de constitution d'un portefeuille deviennent donc :
REGLES DE CONSTITUTION D'UN PORTEFEUILLE
- Déterminer la composition idéale de votre portefeuille pour obtenir le meilleur rapport rendement/risque ;
- Déterminer votre niveau de sensibilité au risque et votre risque maximum acceptable ;
- Régler le levier pour ajuster le risque pris en-dessous de votre risque maximum acceptable.
Et ensuite ?
Pour compléter notre voyage, il nous reste quelques petites choses à voir :
- la ou les solutions permettant de stabiliser les matrices de variance/covariance ;
- la ou les solutions permettant de fiabiliser les espérances de rendements ;
- comment prendre des positions en levier dans la vraie vie ;
- la ou les méthodes permettant de définir notre risque maximum acceptable.
Je vous propose de commencer par ce dernier point en faisant un petit détour par les simulations de Monte Carlo qui devraient nous aider à appréhender le risque en nous en proposant une représentation plus percutante qu'une mesure de volatilité. Rendez-vous donc très bientôt pour la suite de cette saga...
Si vous brûlez de le savoir avant que j'ai eu le temps de rédiger les pages suivantes, vous pouvez vous reporter aux ouvrages suivants :
![]() La Modélisation du risque : Simulations de Monte Carlo
La Modélisation du risque : Simulations de Monte Carlo
![]() Exercices de théorie financière et de gestion de portefeuille
Exercices de théorie financière et de gestion de portefeuille
![]() Gestion de portefeuille
Gestion de portefeuille
![]() La théorie moderne du portefeuille
La théorie moderne du portefeuille
![]() Marchés Financiers - Gestion de portefeuille et des risques
Marchés Financiers - Gestion de portefeuille et des risques
![]() Principes de Finance Moderne
Principes de Finance Moderne
Et si vous avez déjà lu les précédents, vous pouvez aller plus loin avec :
![]() La Nouvelle Finance et la Gestion des Portefeuilles
La Nouvelle Finance et la Gestion des Portefeuilles
![]() The New Finance
The New Finance
![]() Retour au début de la page
Retour au début de la page
![]() Retour au sommaire de l'optimisation
Retour au sommaire de l'optimisation
![]() Retour au sommaire du site
Retour au sommaire du site
Rubriques
Meilleurs courtiers en Bourse
Meilleurs PEA
Toutes les données du CAC40
Livres finance et Bourse
Newsletter
Pour recevoir nos derniers articles, détachements de dividendes et offres de placements :
Nous contacter ou nous suivre sur les réseaux
Site hébergé par OVH - 2 rue Kellermann - 59100 Roubaix - France - Tel : 09 72 10 10 10