Le risque
"RISQUE n. m. (ital. risco). Danger, inconvénient possible : courir un risque ; s'exposer à un risque. || Préjudice, sinistre éventuel, que les compagnies d'assurance garantissent moyennant le paiement d'une prime. || Risque social, perte de l'emploi, diminution du niveau de vie familial, maladie, accident, maternité, invalidité, vieillesse, décès, que la politique moderne de sécurité sociale vise à prévenir ou à réparer. || A tout risque, à tout hasard. || A ses risques et périls, en assumant sur soi toute la responsabilité d'une chose, d'une entreprise. || -- Au risque de loc. prép. Au hasard de, en s'exposant à." Petit Larousse.
Lorsque l'on débute, surtout si le marché est en période haussière, on perçoit très bien les possibilités de gain, mais plutôt mal les risques. Avec l'expérience, on comprend qu'il faut s'intéresser au couple rendement/risque plutôt qu'au rendement seul. On est alors confronté à un triple problème : celui de la nature du risque, celui de sa mesure ou de sa quantification et celui de sa gestion.
Le risque est la pierre maîtresse de l'édifice. L'ignorer revient à courir à une ruine quasi certaine ou à limiter sérieusement ses plus-values. La différence principale entre un particulier et un professionnel, ou au moins un amateur éclairé, réside probablement dans le rapport au risque.
Les pages suivantes se proposent de vous faire découvrir le concept de risque, puis de vous fournir quelques outils simples à mettre en oeuvre, et enfin de vous soumettre quelques liens vous permettant de poursuivre le voyage.
Sommaire
- Types de risques Vous êtes ici !
- Risque de baisse
- Risque de liquidité
- Risque de change
- Appréhender le risque
- Jouer avec les futurs du CAC 40
- Mesure du risque
- La volatilité
- L'écart-type
- Exemple de calcul du risque de deux titres
- Que faire de la volatilité ?
- Le ratio de Sharpe
- Bon, ok pour le passé, mais l'avenir ?
- Gestion du risque : la diversification
- La magie des oeufs et du panier
- La corrélation
- Gestion du risque : la covariance
- La covariance
- Calcul de la covariance
- Calcul de la covariance avec un tableur
- Et après ?
- Gestion du risque : la variance d'un portefeuille
- Variance passée
- Variance future
- Matrice de variances-covariances
- Exemple d'application
- Feuille de calcul de la variance future estimée d'un portefeuille
- Attention !
- Vite la suite...
Types de risques
Le risque est polymorphe. Avant d'aborder sa quantification ou sa gestion, il convient de reconnaître ses différentes formes, natures ou manifestations.
Risque de baisse
Le risque de baisse de la valeur d'un titre se décompose en une partie dite systématique qui correspond au risque global du
marché et en une partie spécifique au titre particulier dite non systématique. Nous verrons plus loin que le risque systèmatique est loin d'être
négligeable puisqu'il est responsable de 73 à 90% du rendement moyen [à reformuler cf p.105 de "Principes de Finance Moderne"].
La diversification au sein d'un portefeuille, si elle est bien menée, permet d'éliminer le risque non systématique.
Risque de liquidité (ou de contrepartie)
Si un titre est peu liquide, il est fort probable qu'un décalage de cours important aura lieu au premier problème.
Il faut toujours garder à l'esprit que pour qu'un échange ait lieu, il faut un accord entre deux parties. Autrement dit, si
vous souhaitez vendre à un prix donné, il faut une contrepartie acceptant d'acheter à ce prix. Si personne ne souhaite
acheter, vous ne pouvez pas vendre ou vous devez accepter de vendre moins cher. Donc si de nombreuses personnes souhaitent
vendre alors même qu'aucun acheteur ne se présente... le cours s'effondre.
Le risque lié à la liquidité est donc loin d'être négligeable.
Risque de change
Le risque de change est lié aux fluctuations des monnaies entre elles, donc aux investissements réalisés en monnaies étrangères . Ainsi, si vous achetez des valeurs sur le NYSE par exemple lorsque le dollar est fort, donc cher par rapport à l' euro, vous risquez de voir vos éventuelles plus-values partir en fumée lorsque vous reconvertirez le fruit de votre vente de dollars en euros si d'ici là le dollar est retombé.
Apprehender le risque
« Le risque suppose qu'il peut se passer plus de choses qu'il ne s'en passera. » Elroy Dimson
Le risque est un concept particulièrement complexe à appréhender pour l'être humain. En effet, il n'est pas possible de prévoir le futur, et lorsque l'on prend un risque, parmi tous ceux qui auraient pu se réaliser, un seul futur deviendra le présent, puis le passé. Il sera alors certain, mais nous ne connaîtrons jamais les multiples futurs possibles qui n'ont jamais pris forme.
Lorsque l'on choisit de placer son capital en Bourse, même si l'on peut gérer le risque pris comme nous le verrons plus loin, ce capital évoluera au fil du temps mais sauf scénario catastrophe, son évolution nous renseignera finalement très peu sur les risques que nous avons pris.
Jouer avec les futurs du CAC 40
Aussi, avant de lire la suite de cette section consacrée au risque, je vous invite à jouer quelques minutes avec notre générateur de futurs du CAC 40. Celui-ci vous permettra d'appréhender le risque d'un investissement sur le CAC 40.
Mesure du risque
La mesure du risque s'effectue en général sur la base du cacul de la volatilité, c'est à dire par l'intermédiaire de la
mesure de l'amplitude des variations.
Et la volatilité se mesure par le biais de l'écart-type des rendements constatés. Pour calculer le risque relatif à un
placement, il va donc vous falloir réviser un peu vos maths ou vous armer d'un tableur.
Ce chapitre se propose d'expliquer ce qu'est la volatilité et comment on la mesure. Un exemple vous permettra ensuite de
vérifier que vous avez compris.
La volatilité
Avant d'aller plus loin, il est intéressant de 'voir' ce qu'est la volatilité. Le graphique ci-dessous vous montre l'évolution de deux titres fictifs, l'un très volatil et l'autre peu volatil. Ces deux titres valent 100 au départ, 110 à la fin, ont tous deux une moyenne arithmétique de 105,52. A partir de ces trois critères, ils sont identiques. Toutefois, on voit bien qu'ils sont différents puisqu'ils ont fluctués de manière totalement différente. L'écart type nous renseigne sur ces fluctuations puisque il est égal à 16,24% pour le premier et à 1,32% seulement pour le second.
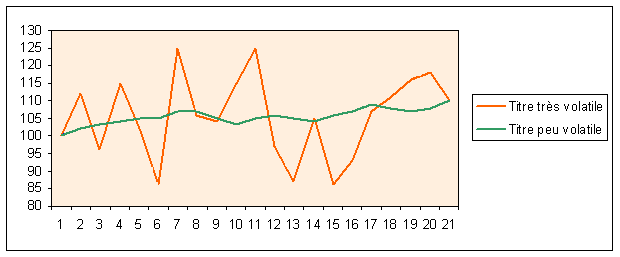
On voit bien ici que l'écart-type renseigne sur les fluctuations d'une valeur. Le titre rouge fluctue beaucoup plus que le titre vert. L'écart type du titre rouge est largement supérieur à celui du titre vert.
L'écart-type
Si les maths vous rebutent, vous pouvez sauter ce paragraphe en vous contentant de retenir que tous les tableurs proposent une formule de calcul de l'écart-type. Il s'agit par exemple de 'ECARTYPEP()' dans Excel. Pour les autres, voici le mode de calcul de l'écart type.
L'écart-type est égal à la racine carrée de la variance :
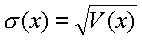
...et la variance est égale à la somme des carrés des distances entre les différentes valeurs de l'échantillon et la moyenne :
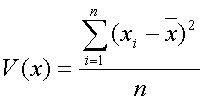 où
où 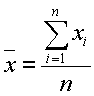 , c'est à dire la moyenne.
, c'est à dire la moyenne.
Le fait de prendre la somme des carrés des distances présente l'avantage d'augmenter proportionnellement le poids des
écarts entre chaque élément et la moyenne. Ainsi, plus l'écart est important, plus son carré est important.
L'image animée ci-dessous illustre le mode de calcul de la variance :
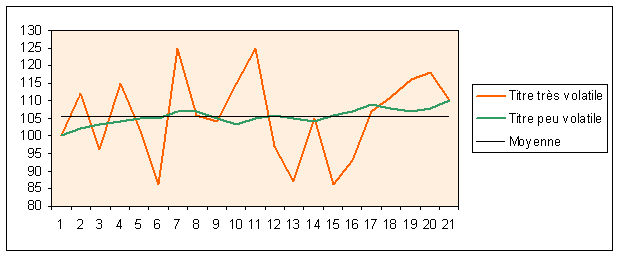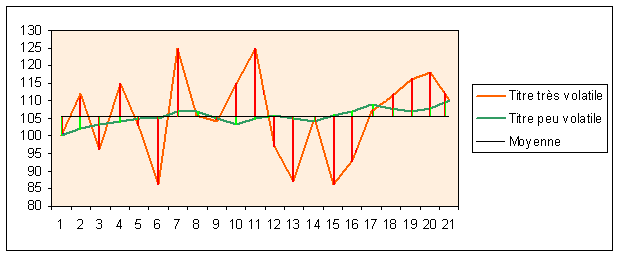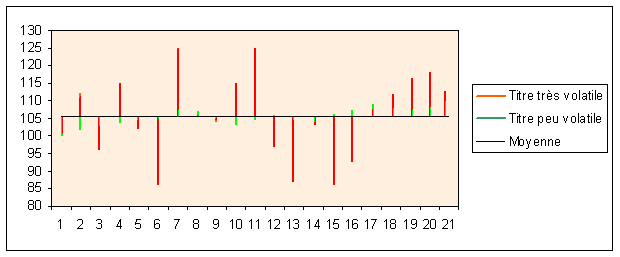
Dans un premier temps, on calcule et affiche la moyenne (ligne horizontale noire).
Dans un second temps, on calcule les distances entre les valeurs et la moyenne (segments verticaux rouges et verts).
Dans notre exemple, la variance, donc la somme des carrés des écarts est égale pour le titre très volatil à la somme des
carrés des distances en rouge et pour le titre peu volatil à la somme des carrés des distances vertes.
Le graphique n'affiche que les distances. Le carré de celles-ci serait beaucoup plus important et rendrait les segments verts
pratiquement illisibles.
Exemple de calcul du risque de deux titres
Pour appliquer ce que nous venons de voir, je vous propose d'essayer de calculer la volatilité de deux titres du CAC40 sur
les douze derniers mois. Normalement, il faudrait prendre une fréquence hebdomadaire pour disposer d'un échantillon
suffisament représentatif. Toutefois, pour les besoins de l'exemple, nous baserons les calculs sur les rendements mensuels de
chaque titre.
Les deux valeurs retenues sont AGF et Canal + car elles figurent aux opposés. Voici leurs courbes de fin 1999 à fin 2000 :
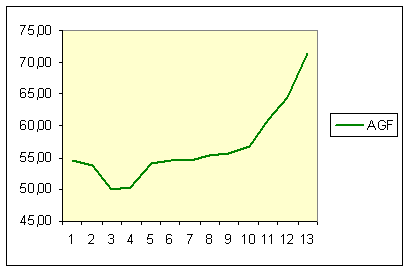
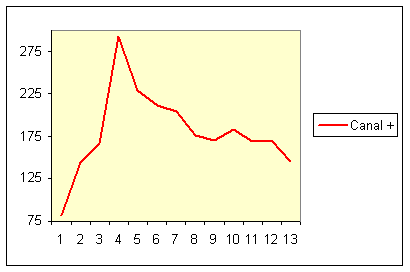
Celles-ci sont telles qu'on peut les visualiser dans un logiciel d'analyse technique, c'est à dire que chacune dispose de
sa propre échelle verticale (axe des prix).
Les cours à la fin de chaque mois sont les suivants :
| Date | Cours AGF | Variation | Ecart de la variation à la moyenne |
Carré de l'écart | Cours Canal + | Variation | Ecart de la variation à la moyenne |
Carré de l'écart |
|---|---|---|---|---|---|---|---|---|
| mardi 30/11/1999 | 54,60 | 82,10 | ||||||
| jeudi 30/12/1999 | 53,80 | 1 | 3 | 4 | 144,50 | 1 | 3 | 4 |
| lundi 31/01/2000 | 50,15 | 1 | 3 | 4 | 166,50 | 1 | 3 | 4 |
| mardi 29/02/2000 | 50,20 | 1 | 3 | 4 | 293,00 | 1 | 3 | 4 |
| vendredi 31/03/2000 | 54,05 | 1 | 3 | 4 | 230,00 | 1 | 3 | 4 |
| vendredi 28/04/2000 | 54,65 | 1 | 3 | 4 | 212,00 | 1 | 3 | 4 |
| mercredi 31/05/2000 | 54,50 | 1 | 3 | 4 | 204,00 | 1 | 3 | 4 |
| vendredi 30/06/2000 | 55,35 | 1 | 3 | 4 | 176,00 | 1 | 3 | 4 |
| lundi 31/07/2000 | 55,70 | 1 | 3 | 4 | 171,00 | 1 | 3 | 4 |
| jeudi 31/08/2000 | 56,80 | 1 | 3 | 4 | 183,90 | 1 | 3 | 4 |
| vendredi 29/09/2000 | 61,00 | 1 | 3 | 4 | 169,70 | 1 | 3 | 4 |
| mardi 31/10/2000 | 64,50 | 1 | 3 | 4 | 170,50 | 1 | 3 | 4 |
| jeudi 30/11/2000 | 71,50 | 1 | 3 | 4 | 145,50 | 1 | 3 | 4 |
| Moyenne des variations | 2 | 2 | ||||||
| Moyenne des carrés des écarts | 5 | 5 | ||||||
| Ecart-Type | 6 | 6 |
Je vous propose de remplir ensemble les cases vides du tableau ci-dessus, en 6 étapes. Pour pouvoir comparer la volatilité de différentes
valeurs entre elles, on calculera l'écart-type de leurs variations de cours, plutôt que l'écart type de leurs cours.
1 Calculer les variations de cours :
Pour AGF par exemple, la variation au 30/12/1999 est égale à ((53,80/54,60)-1)*100, soit -1,47%.
Calculez les variations de cours d'AGF et de Canal +...
2 Calculer la moyenne des variations de cours :
Pour AGF par exemple, la moyenne sera de 2,38%.
Calculez la moyenne des variations pour Canal +...
3 Calculer les écarts des variations à la moyenne :
Pour AGF toujours, l'écart à la moyenne au 30/12/1999 sera de -1,47%-2,38%, soit -3,85% (le tableau ci-dessous affiche
-3,84% car les données sont issues d'un tableur, la précision va donc au-delà de deux chiffres).
Calculez les écarts à la moyenne d'AGF et de Canal +...
4 Calculer les carrés des écarts :
Toujours pour AGF, le carré de l'écart au 30/12/1999 est égal à (-3,84%)*(-3,84%), soit 0,15%. Attention, je vous
rappelle que 1% est égal à 0,01 et non pas à 1.
Calculez les carrés des écarts d'AGF et de Canal +...
5 Calculer la moyenne des carrés des écarts, c'est à dire la variance :
La moyenne des carrés des écarts est égale à 0,21% pour AGF.
Calculez la moyenne des carrés des écarts pour Canal+.
6 Calculer la racine carrée de la variance, c'est à dire l'écart-type :
Pour AGF, racine(0,21%)=4,59%.
Calculez l'écart-type de Canal+ de la même manière.
En prime, on peut même calculer l'écart-type annuel. Il faut alors multiplier l'écart-type mensuel par la racine carrée
de 12 puisqu'il y'a douze mois dans l'année.
| Date | Cours AGF | Variation | Ecart de la variation à la moyenne |
Carré de l'écart | Cours Canal + | Variation | Ecart de la variation à la moyenne |
Carré de l'écart |
|---|---|---|---|---|---|---|---|---|
| mardi 30/11/1999 | 54,60 | 82,10 | ||||||
| jeudi 30/12/1999 | 53,80 | -1,47% | -3,84% | 0,15% | 144,50 | 76,00% | 67,41% | 45,44% |
| lundi 31/01/2000 | 50,15 | -6,78% | -9,16% | 0,84% | 166,50 | 15,22% | 6,63% | 0,44% |
| mardi 29/02/2000 | 50,20 | 0,10% | -2,28% | 0,05% | 293,00 | 75,98% | 67,38% | 45,40% |
| vendredi 31/03/2000 | 54,05 | 7,67% | 5,29% | 0,28% | 230,00 | -21,50% | -30,10% | 9,06% |
| vendredi 28/04/2000 | 54,65 | 1,11% | -1,27% | 0,02% | 212,00 | -7,83% | -16,42% | 2,70% |
| mercredi 31/05/2000 | 54,50 | -0,27% | -2,65% | 0,07% | 204,00 | -3,77% | -12,37% | 1,53% |
| vendredi 30/06/2000 | 55,35 | 1,56% | -0,82% | 0,01% | 176,00 | -13,73% | -22,32% | 4,98% |
| lundi 31/07/2000 | 55,70 | 0,63% | -1,74% | 0,03% | 171,00 | -2,84% | -11,44% | 1,31% |
| jeudi 31/08/2000 | 56,80 | 1,97% | -0,40% | 0,00% | 183,90 | 7,54% | -1,05% | 0,01% |
| vendredi 29/09/2000 | 61,00 | 7,39% | 5,02% | 0,25% | 169,70 | -7,72% | -16,32% | 2,66% |
| mardi 31/10/2000 | 64,50 | 5,74% | 3,36% | 0,11% | 170,50 | 0,47% | -8,13% | 0,66% |
| jeudi 30/11/2000 | 71,50 | 10,85% | 8,48% | 0,72% | 145,50 | -14,66% | -23,26% | 5,41% |
| Moyenne des variations | 2,38% | 8,60% | ||||||
| Moyenne des carrés des écarts | 0,21% | 9,97% | ||||||
| Ecart-Type | 4,59% | 31,57% | ||||||
| Ecart-Type annualisé | 15,90% | 109,36% |
On constate donc que la volatilité de l'action AGF a été largement inférieure à celle de l'action Canal+ en 2000. Ce qui se confirme visuellement si l'on regarde les deux titres à la même échelle sur un graphique :
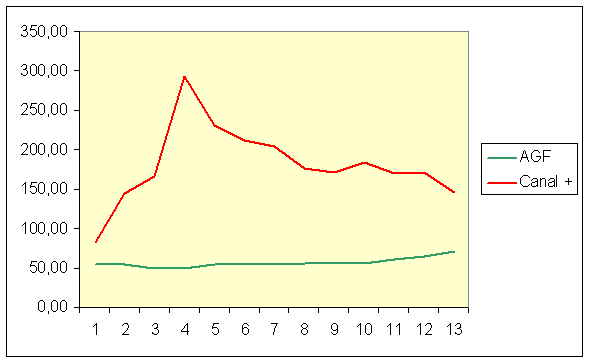
La courbe d'AGF est sans conteste beaucoup moins heurtée que celle de Canal+.
Que faire de la volatilité ?
Attention : cette partie est partagée avec la page de méta-méthode. Si vous l'avez déjà lue, vous pouvez éventuellement la sauter.
En tant qu'amateur, on a souvent tendance à ne considérer que la performance et à juger les différentes valeurs en fonction du seul axe du rendement passé ou plutôt du rendement attendu. Notre outil de mesure ressemble alors à celui-ci :
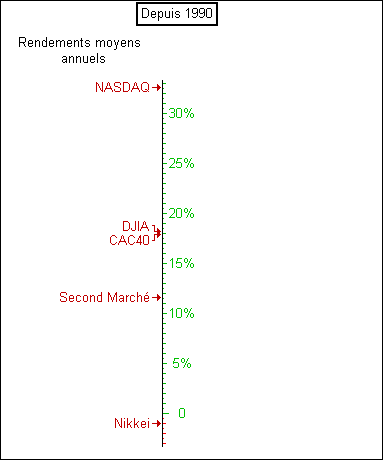
D'après ce graphique, le NASDAQ avec plus de 30% de rendements annuels depuis presque dix ans constitue clairement le meilleur des investissements. La volatilité nous offre un nouvel axe de vision. Si l'on regarde les écart-types des rendements, donc les risques, obtenus par ces mêmes indices pendant la même durée, on obtient la vision suivante :

Sur le plan des risques, c'est plutôt le Dow Jones (DJIA) qui semble le mieux placé ou du moins le moins risqué
sur la même période.
Et si l'on assemble les deux côtés du graphique, on obtient un thermomètre pour le moins étrange :

Dès lors, comment concilier ces deux visions ?
Le plus simple consiste à les représenter selon deux axes différents :
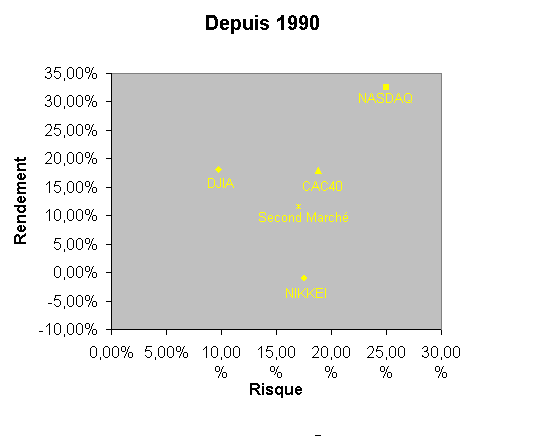
Ce type de graphique nous en apprend déjà davantage : sur les dix dernières années, si le Nasdaq a été le plus
rémunérateur de nos cinq indices, il a aussi été le plus risqué (et il suffit de considérer sa performance en 2000 pour
s'en convaincre et comprendre que la théorie a quelques connexions avec la réalité).
Quant aux CAC40 et Dow Jones (DJIA), leur comparaison est elle-aussi très instructive puisqu'on constate qu'ils ont offerts pratiquement le même rendement, mais assorti d'un
risque beaucoup plus important pour le CAC que pour le DJIA.
L'important ici est de prendre conscience du risque et de comprendre qu'au-delà de la performance, il existe une autre
dimension toute aussi importante : le risque. Tout investissement, tout portefeuille doit-être mesuré selon ces deux
axes. Il est donc primordial de savoir à quel niveau de risque on s'expose ou on s'est exposé. Non pas obligatoirement
pour opter pour l'avoir le moins risqué, mais pour être conscient de ce que l'on fait et de ce que l'on risque (sic!) !
Si une prime est souvent offerte au risque (cf Nasdaq ici), ce n'est pas systèmatiquement le cas, il suffit de regarder
le Nikkei pour s'en convaincre...
Vous savez maintenant calculer le risque et le rendement et les représenter sur un graphique. Mais si l'on voit bien sur le graphique ci-dessus qu'il valait mieux posséder du Nasdaq que du Nikkeï sur les dix dernières années, le Dow Jones était-il plus intéressant que le Nasdaq ou inversement ?
Puiqu'il est possible de calculer un rendement et un risque, peut-être est-il possible de calculer un mélange des deux ? Comme vous devez vous en douter, c'est possible, le ratio de Sharpe sert justement à cela et permet de comparer différents véhicules d'investissements (indices, valeurs, portefeuilles) en fonction de leurs couples rendement/risque.
Le ratio de Sharpe
Le ratio de Sharpe permet donc de comparer différents placements en fonction de leurs couples rendement/risque. Il est très
simple à calculer et présente de plus l'avantage de tenir compte du placement sans risque.
Le placement sans risque est le taux auquel vous auriez pu placer votre argent sans risque.
La formule de calcul du ratio de Sharpe est la suivante :
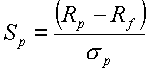
Où :
- Sp
- ratio de Sharpe d'un Portefeuille par exemple
- Rp
- Rendement du portefeuille
- Rf
- Rendement de l'avoir sans risque
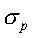
- Ecart-type du portefeuille (risque du portefeuille).
Il ressort immédiatement de cette formule que :
- Tout ratio de Sharpe négatif indique un placement dont le rendement a été inférieur à celui de l'avoir sans risque ;
- Tout ratio de Sharpe inférieur à 1 indique un placement dont l'excédent de rendement par rapport au taux sans risque est inférieur au risque pris ;
- Un ratio de Sharpe plus élevé est "meilleur" qu'un ratio de Sharpe bas.
Le calcul du ratio de Sharpe pour les différents indices représentés donne (en prenant un avoir sans risque moyen de 4%):
| Indice | Ratio de Sharpe |
|---|---|
| DJIA | 1,46 |
| Nasdaq | 1,15 |
| CAC40 | 0,74 |
| Second Marché | 0,45 |
| Nikkeï | -0,29 |
On retrouve bien dans ce tableau les mêmes résultats que ceux constatés en regardant le schéma précédent. La différence,
c'est qu'il est plus facile (surtout pour un ordinateur) de comparer des nombres que des graphiques !
Par ailleurs, vu le ratio de Sharpe du Dow Jones (DJIA) comparé à celui du Nasdaq, il aurait mieux valu sur les neuf
dernières années acheter du Dow Jones que du Nasdaq, quitte à prendre du levier. Le risque aurait été moins important.
En guise de conclusion de cette première partie, la règle suivante pourra être retenue :
REGLE
Toute prise de position comporte deux faces : l'espérance de rendement et le RISQUE.
Bon, ok pour le passé, mais l'avenir ?
Tout ça, c'est bien joli, ça permet de calculer plein de choses intéressantes au sujet du passé, mais l'avenir ?
La suite du voyage dans la deuxième partie : Gestion du risque.
![]() Retour au début de la page
Retour au début de la page
![]() Page suivante sur le risque
Page suivante sur le risque
![]() Retour au sommaire du site
Retour au sommaire du site
Rubriques
Meilleurs courtiers en Bourse
Meilleurs PEA
Toutes les données du CAC40
Livres finance et Bourse
Newsletter
Pour recevoir nos derniers articles, détachements de dividendes et offres de placements :
Nous contacter ou nous suivre sur les réseaux
Site hébergé par OVH - 2 rue Kellermann - 59100 Roubaix - France - Tel : 09 72 10 10 10