Gestion du risque : la covariance
Préambule : un grand merci à François C. dont la perspicacité a permis la correction d'une grossière erreur d'étourderie dans cette page.
Au cours du chapitre précédent, nous avons vu que le risque, ou au moins la volatilité, d'un portefeuille de titres est
inférieure à la moyenne des risques de chaque titre. Les différents titres composants le portefeuille ne fluctuent pas
de manière identique : ils sont partiellement décorrélés.
Pour pouvoir calculer le risque lié à un portefeuille, plusieurs méthodes existent. Concernant le risque passé, il suffit
de mesurer la volatilité de ses rendements. Par contre, pour pouvoir estimer son risque futur, il faut s'attaquer à un
calcul un peu plus musclé
permettant de tenir compte à la fois de l'amplitude des variations des différents titres, mais aussi à leurs corrélations
respectives.
Ce calcul nécessite quelques bases, dont la principale est la notion de covariance. Je vous invite donc dans cette page
à découvrir le concept de covariance. Si vous le connaissez déjà, ou si les calculs rébarbatifs vous ennuient, vous pouvez
passer directement à la suite.
La covariance
La covariance de deux séries de données est la moyenne des aires des rectangles définis par chaque couple de données et la moyenne des deux séries :
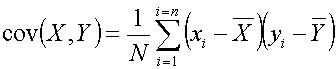
Gloups ! Un peu sec non ?
Reprenons : la covariance mesure la corrélation de deux séries de données. Plus elle est faible, plus les séries
sont indépendantes. A l'inverse, plus la covariance est élevée, plus les séries sont liées.
Si vous vous souvenez de la première page sur le risque, la variance était la somme des carrés des distances séparant chaque
point de la moyenne. La covariance entre deux séries de données est calculée d'une manière similaire.
Prenons un exemple et essayons de calculer la covariance des variations des titres Carrefour et Renault sur les 12
derniers mois.
Les valeurs en question ont fluctués de :
| Mois | Carrefour | Renault |
|---|---|---|
| Mai 2000 | +5,94% | +1,00% |
| Juin 2000 | -5,60% | -5,74% |
| Juillet 2000 | +10,89% | -2,63% |
| Août 2000 | +3,40% | +5,63% |
| Septembre 2000 | +1,95% | -0,74% |
| Octobre 2000 | -5,50% | +20,58% |
| Novembre 2000 | -12,45% | -6,31% |
| Décembre 2000 | -3,39% | +1,09% |
| Janvier 2001 | -0,07% | -2,16% |
| Février 2001 | -5,09% | +7,55% |
| Mars 2001 | -2,60% | -1,88% |
| Avril 2001 | +5,26% | +1,13% |
| Moyenne | -0,61% | +1,46% |
Le tableau se lit de la manière suivante : lorsque Carrefour s'est apprécié de 5,94% en mai 2000, Renault ne s'est quant à lui apprécié que de 1%. Il nous donne ainsi douze couples de valeurs définissant douze points, ainsi qu'un treizième pour la moyenne. Si l'on représente ces treize points de manière graphique en prenant Carrefour pour abscisse et Renault pour ordonnée, on obtient le graphe ci-dessous :
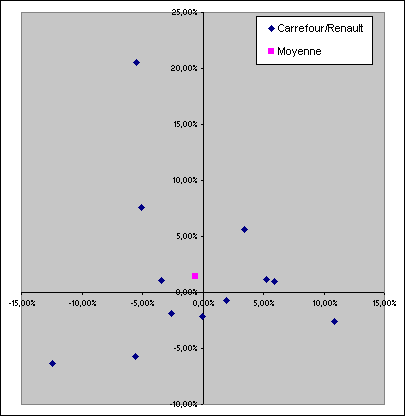
On constate de visu que Carrefour et Renault n'ont pas l'air d'être particulièrement corrélées. Les points ne se situent pas tous sur le même axe. Reste à savoir comment calculer la covariance car encore une fois, avec un ordinateur, il est plus facile de comparer des nombres que des graphiques.
Calculer comme pour la variance d'une série la somme des carrés des distances de chaque point à la moyenne donnerait un résultat toujours positif et une indication sur l'éparpillement des données mais pas sur leur corrélation. Il faut donc trouver un autre moyen.
Peut-être en prenant les rectangles définis par chaque point et le point moyen ?
Prenons par exemple le point en haut à gauche représentant le mois d'octobre 2000. Ce point est à l'intersection de x = -5,50%
c'est à dire la dépréciation de Carrefour ce mois là et y = +20,58% qui représente l'appréciation de Renault pour ce mois.
Nous allons dessiner un rectangle entre ce point et le point 'moyen' de coordonnées (-0,61 , 1,46). Et nous colorierons ce
rectangle en rouge car il est 'négatif'. En effet, le gain de Carrefour ce mois là se situe sous sa moyenne (-5,50 est
inférieur à -0,61) alors que celui de Renault se situe au-dessus (20,58 est supérieur à 1,46). Carrefour et Renault ont donc
fluctués à l'inverse au mois d'octobre 2000. Ils étaient corrélés négativement.
Prenons ensuite le point en haut à droite représentant le mois d'août 2000, point à l'intersection de x = 3,40 et y = 5,63 et dessinons un rectangle entre ce point et le point 'moyen'. Nous colorierons ce rectangle en bleu car il est 'positif', en effet, les deux valeurs Carrefour et Renault ont progressé au mois d'août 2000 tous les deux davantage que leurs moyennes respectives. Ils étaient donc positivement corrélés.
Si l'on trace ainsi les douze rectangles, on obtient le graphe suivant :
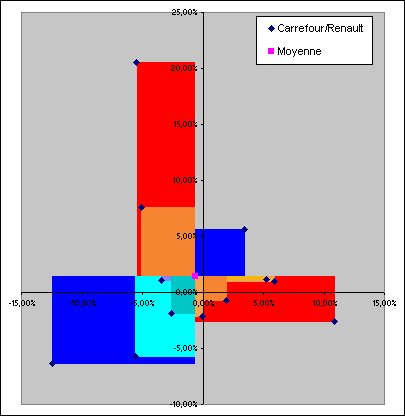
Les rectangles situés en haut à gauche et en bas à droite de la moyenne sont représentés dans des teintes rouges car ils représentent des variations décorrélées entre elles (ces mois là, Carrefour et Renault n'ont pas varié dans le même sens). A l'inverse, les rectangles situés en haut à droite et en bas à gauche de la moyenne sont représentés dans des teintes bleues car ils représentent des variations corrélées entre elles (ces mois là, Carrefour et Renault ont varié de concert).
On voit ici encore mieux que la somme des superficies des rectangles rouges est assez proche de celle des rectangles bleus. Carrefour et Renault sont donc probablement assez peu corrélées.
Avant de le vérifier par le calcul, je vous propose d'étudier un autre couple de valeurs : France Télécom et STMicroelectronics. Ces deux valeurs sont à priori très corrélées entre elles. Voici le nuage de points obtenus en traçant leurs variations :
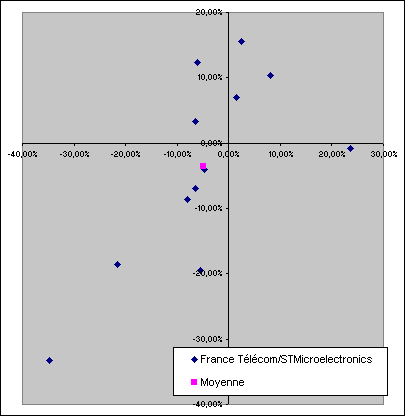
On remarque ici que les points se répartissent beaucoup plus selon un axe allant du bas à gauche au haut à droite, ce qui est typique d'une corrélation fortement positive (deux valeurs fluctuant de concert). Si l'on trace les rectangles pour le vérifier, on obtient...
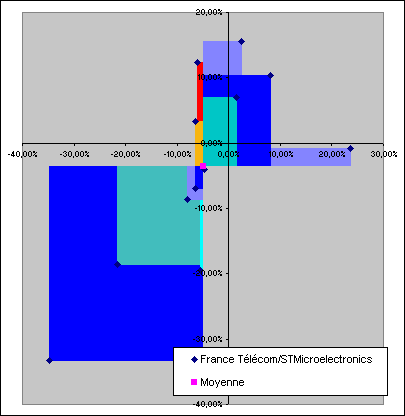
...beaucoup de bleu, comme prévu ! Sur douze échantillons, France Télécom et STMicroelectronics n'ont fluctuées à l'envers l'une de l'autre que trois fois.
Avec les deux couples de valeurs observés, nous avons vu une première dimension permettant de déterminer si deux valeurs
sont corrélées entre elles (positivement ou négativement) ou si elles ne le sont pas.
Mais comment exprimer la force de la corrélation ?
Si on représente les deux graphes déjà vu mais à la même échelle cette fois, on voit bien alors que la surface moyenne des
rectangles dessinés par le couple Carrefour/Renault est beaucoup plus petite que celle des rectangles dessinés par le
couple France Télécom/STMicroelectronics :
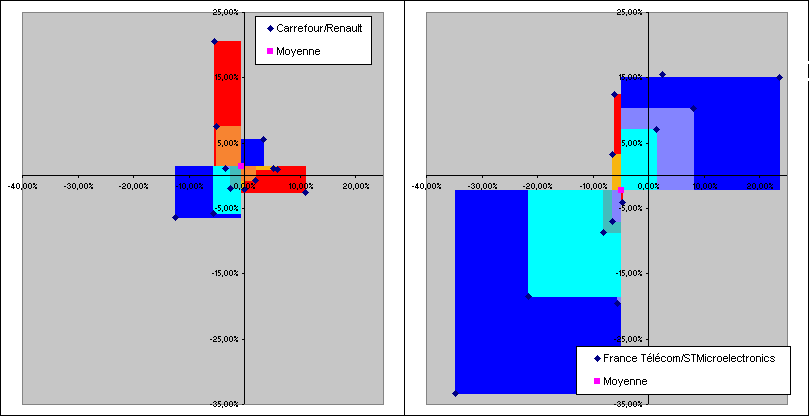
Bien, on a donc maintenant toutes les dimensions. Reprenons nos deux exemples et animons les :
- On cumule les rectangles bleus pour chaque couple de valeurs.
- On retranche les rectangles rouges pour chaque couple toujours.
- On regroupe la superficie restante en un rectangle de chaque côté.
- On divise la surface restante par le nombre de rectangles (12 dans notre cas).
- On a notre covariance. Plus le rectangle restant est gros, plus les valeurs sont corrélées.
Si le rectangle est rouge, les valeurs sont négativement corrélées entre elles (elles fluctuent à l'envers l'une de l'autre), par contre, si le rectangle est bleu, les valeurs sont positivement corrélées entre elles (elles fluctuent de concert).
Puisqu'on a douze couples de valeurs dans notre exemple, on peut se contenter deux premières étapes et comparer les superficies restantes sans avoir besoin de les regrouper et de les diviser par 12. Ce qui nous donne (attendre quelques secondes pour voir l'animation) :
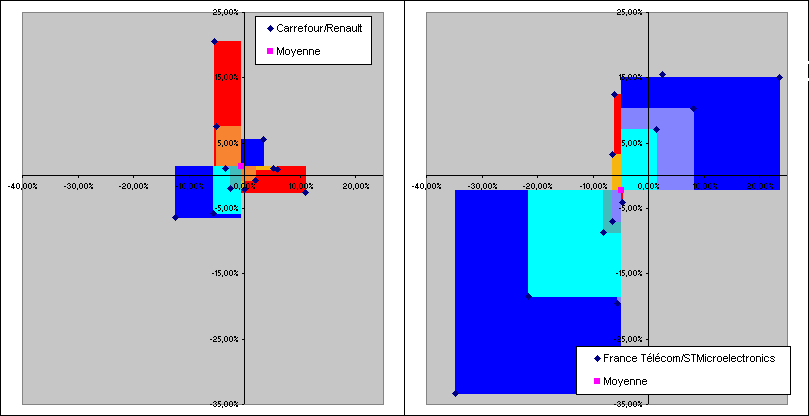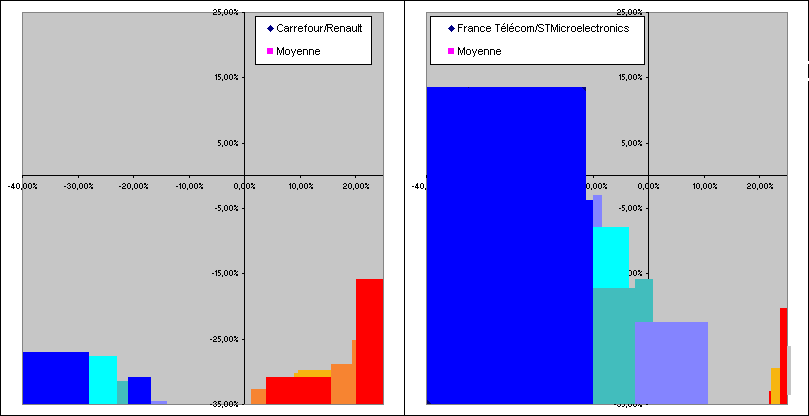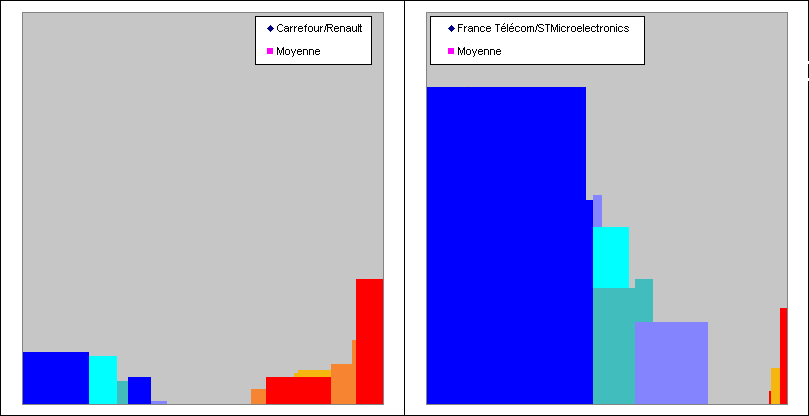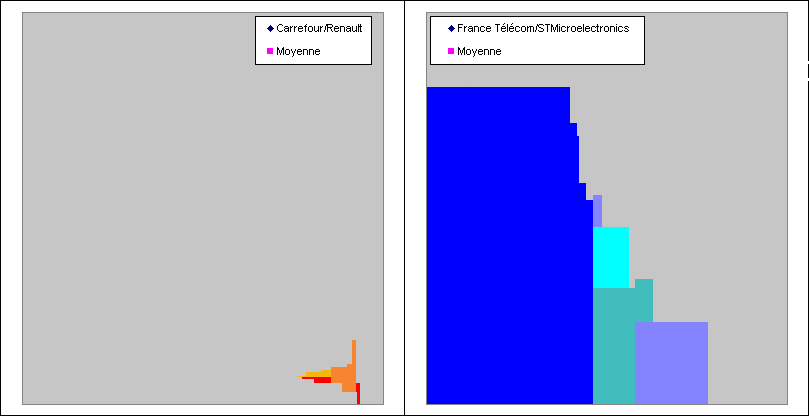
Dans notre exemple, on peut donc dire que Carrefour et Renault sont faiblement négativement corrélées et que France Télécom et STMicroelectronics sont fortement positivement corrélées.
Calcul de la covariance
Après avoir étudié géométriquement ce qu'est la covariance, nous allons essayer de la calculer arithmétiquement.
Selon la formule exposée plus haut et rappelée ci-dessous, la covariance de deux titres est la moyenne des aires des rectangles définis par chaque couple de variations et la moyenne des deux séries de variations :
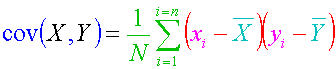
Vous pouvez maintenant appliquer la formule et calculer la covariance entre les valeurs Carrefour et Renault en remplissant le tableau suivant :
| Période | Carrefour | Renault | Rectangle |
|---|---|---|---|
| Mai 2000 | 1 | 2 | 4 |
| Juin 2000 | 1 | 2 | 4 |
| Juillet 2000 | 1 | 2 | 4 |
| Août 2000 | 1 | 2 | 4 |
| Septembre 2000 | 1 | 2 | 4 |
| Octobre 2000 | 1 | 2 | 4 |
| Novembre 2000 | 1 | 2 | 4 |
| Décembre 2000 | 1 | 2 | 4 |
| Janvier 2001 | 1 | 2 | 4 |
| Février 2001 | 1 | 2 | 4 |
| Mars 2001 | 1 | 2 | 4 |
| Avril 2001 | 1 | 2 | 4 |
| Moyenne | 3 | 3 | |
| Moyenne, ou covariance | 5 | ||
1 Reportez dans un premier temps les variations mensuelles de l'action Carrefour (cf tableau en haut de page). Les variations seront
exprimées arithmétiquement et non pas par un pourcentage. Par exemple pour le mois de mai 2000, la variation a été de
5,94%, ce qui fera donc 0,0594.
2 Faites de même pour les variations de l'action Renault. Ce qui nous donnera par exemple pour le mois de
mai 2000 une valeur de 0,0100.
3 Calculez les moyennes des variations mensuelles de chaque valeur. Ces moyennes nous serviront ensuite à
caluler la covariance.
4 Calculez maintenant pour chaque mois la covariance entre les deux titres. Il suffit de calculer l'aire
du rectangle formé par leurs variations du mois et leurs variations moyennes. La formule est donc :
(variation du mois Carrefour - moyenne des variations de Carrefour) * (variation du mois de Renault - moyenne des variations de Renault)
ce qui donne par exemple pour le mois de mai 2000 : ( 0,0594+0,0061) * ( 0,0100-0,0146), c'est à dire -0,00030099.
5 Calculez maintenant la moyenne des covariances calculées à l'étape précédente. Vous avez maintenant la
covariance des deux titres Carrefour et Renault sur la période considérée.
Une fois l'exercice réalisé, on obtient le tableau suivant :
| Période | Carrefour | Renault | Rectangle |
|---|---|---|---|
| Mai 2000 | 0,0594 | 0,0100 | ( 0,0594-(-0,0061)) * ( 0,0100-0,0146) = -0,00030 |
| Juin 2000 | -0,0560 | -0,0574 | (-0,0560-(-0,0061)) * (-0,0574-0,0146) = 0,00360 |
| Juillet 2000 | 0,1089 | -0,0263 | ( 0,1089-(-0,0061)) * (-0,0263-0,0146) = -0,00470 |
| Août 2000 | 0,0340 | 0,0563 | ( 0,0340-(-0,0061)) * ( 0,0563-0,0146) = 0,00167 |
| Septembre 2000 | 0,0195 | -0,0074 | ( 0,0195-(-0,0061)) * (-0,0074-0,0146) = -0,00056 |
| Octobre 2000 | -0,0550 | 0,2058 | (-0,0550-(-0,0061)) * ( 0,2058-0,0146) = -0,00935 |
| Novembre 2000 | -0,1245 | -0,0631 | (-0,1245-(-0,0061)) * (-0,0631-0,0146) = 0,00921 |
| Décembre 2000 | -0,0339 | 0,0109 | (-0,0339-(-0,0061)) * ( 0,0109-0,0146) = 0,00010 |
| Janvier 2001 | -0,0007 | -0,0216 | (-0,0007-(-0,0061)) * (-0,0216-0,0146) = -0,00019 |
| Février 2001 | -0,0509 | 0,0755 | (-0,0509-(-0,0061)) * ( 0,0755-0,0146) = -0,00273 |
| Mars 2001 | -0,0260 | -0,0188 | (-0,0260-(-0,0061)) * (-0,0188-0,0146) = 0,00067 |
| Avril 2001 | 0,0526 | 0,0113 | ( 0,0526-(-0,0061)) * ( 0,0113-0,0146) = -0,00019 |
| Moyenne | -0,0061 | 0,0146 | |
| Moyenne, ou covariance | -0,00023 | ||
Ce résultat confirme l'observation géométrique précédente. Les deux titres sont bien faiblement anti-corrélés. La covariance est en effet négative, ce qui montre l'anti-corrélation.
Nous pouvons maintenant calculer la covariance des titres France Télécom et ST Microélectronics :
| Période | France Télécom | ST Microélectronics | Rectangle |
|---|---|---|---|
| Mai 2000 | -0,0805 | -0,0866 | (-0,0805-(-0,0486)) * (-0,0866-(-0,0228)) = 0,00204 |
| Juin 2000 | -0,0645 | 0,0329 | (-0,0645-(-0,0486)) * ( 0,0329-(-0,0228)) = -0,00089 |
| Juillet 2000 | -0,0649 | -0,0697 | (-0,0649-(-0,0486)) * (-0,0697-(-0,0228)) = 0,00077 |
| Août 2000 | -0,0614 | 0,1238 | (-0,0614-(-0,0486)) * ( 0,1238-(-0,0228)) = -0,00188 |
| Septembre 2000 | -0,0553 | -0,1949 | (-0,0553-(-0,0486)) * (-0,1949-(-0,0228)) = 0,00115 |
| Octobre 2000 | 0,0148 | 0,0702 | ( 0,0148-(-0,0486)) * ( 0,0702-(-0,0228)) = 0,00590 |
| Novembre 2000 | -0,2167 | -0,1850 | (-0,2167-(-0,0486)) * (-0,1850-(-0,0228)) = 0,02727 |
| Décembre 2000 | -0,0472 | -0,0402 | (-0,0472-(-0,0486)) * (-0,0402-(-0,0228)) = -0,00002 |
| Janvier 2001 | 0,0799 | 0,1032 | ( 0,0799-(-0,0486)) * ( 0,1032-(-0,0228)) = 0,01620 |
| Février 2001 | -0,3484 | -0,3333 | (-0,3484-(-0,0486)) * (-0,3333-(-0,0228)) = 0,09311 |
| Mars 2001 | 0,0255 | 0,1550 | ( 0,0255-(-0,0486)) * ( 0,1550-(-0,0228)) = 0,01317 |
| Avril 2001 | 0,2359 | 0,1506 | ( 0,2359-(-0,0486)) * ( 0,1506-(-0,0228)) = 0,04934 |
| Moyenne | -0,0486 | -0,0228 | |
| Moyenne, ou covariance | 0,01718 | ||
Ici encore, le calcul confirme les observations géométriques : durant la période considérée, les valeurs France Télécom et ST Microélectronics ont bien fluctué de concert (la covariance est positive) et ce de manière beaucoup plus marquée que le couple Carrefour, Renault (la covariance est 74,4 fois plus importante).
Calcul de la covariance avec un tableur
Tous les tableurs dignes de ce nom permettent de calculer des covariances. Avec Excel par exemple, c'est la fonction
COVARIANCE ( matrice1 ; matrice2 ) qui permet de le faire.
Elle prend en paramètres deux matrices représentant les séries de données. Si vous souhaitez vérifier les covariances calculées plus haut, vous pouvez saisir dans une feuille de calcul les différentes séries de rendements mensuels et appliquer la formule. Il suffit par exemple pour Carrefour et Renault de :
- saisir les cours de fin de mois de Carrefour dans les cellules B3 à B15 ;
- saisir les cours de fin de mois de Renault dans les cellules D3 à D15 ;
- saisir la formule =B4/B3-1 dans la cellule C4 ;
- copier cette cellule dans les cellules C5 à C15 puis E4 à E15. Les cellules C4:C15 et E4:E15 contiennent maintenant les variations mensuelles des titres Carrefour et Renault pour les 12 mois considérés ;
- saisir la formule =COVARIANCE ( C4:C15 ; E4:E15 ) dans la cellule G18. Vous obtiendrez dans cette cellule la covariance des deux séries de données.
Vous pouvez télécharger la feuille Excel associée si vous le souhaitez.
Et après ?
Maintenant que nous sommes armés du pouvoir de calcul de la covariance, nous allons pouvoir évaluer le risque futur d'un portefeuille. C'est ce que je vous propose de faire dans la quatrième partie de cette saga : le calcul de la variance attendue d'un portefeuille.
![]() Retour au début de la page
Retour au début de la page
![]() Page suivante sur le risque
Page suivante sur le risque
![]() Retour au sommaire du risque
Retour au sommaire du risque
![]() Retour au sommaire du site
Retour au sommaire du site
Rubriques
Meilleurs courtiers en Bourse
Meilleurs PEA
Toutes les données du CAC40
Livres finance et Bourse
Newsletter
Pour recevoir nos derniers articles, détachements de dividendes et offres de placements :
Nous contacter ou nous suivre sur les réseaux
Site hébergé par OVH - 2 rue Kellermann - 59100 Roubaix - France - Tel : 09 72 10 10 10